Please provide the detailed and step by step solution for the following problem:

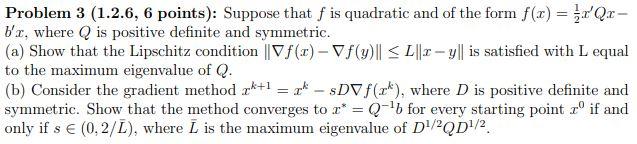
Problem 3 (1.2.6, 6 points): Suppose that f is quadratic and of the form f(x) = 3.x'Qc- b'r, where Q is positive definite and symmetric. (a) Show that the Lipschitz condition || V f() - Vf(y)| SL ||1 - y|| is satisfied with L equal to the maximum eigenvalue of Q. (b) Consider the gradient method rk+1 = - DV f(zk), where D is positive definite and symmetric. Show that the method converges to r* = Q-15 for every starting point t if and only if s (0.2/L), where I is the maximum eigenvalue of D'/?QD1/2. Problem 3 (1.2.6, 6 points): Suppose that f is quadratic and of the form f(x) = 3.x'Qc- b'r, where Q is positive definite and symmetric. (a) Show that the Lipschitz condition || V f() - Vf(y)| SL ||1 - y|| is satisfied with L equal to the maximum eigenvalue of Q. (b) Consider the gradient method rk+1 = - DV f(zk), where D is positive definite and symmetric. Show that the method converges to r* = Q-15 for every starting point t if and only if s (0.2/L), where I is the maximum eigenvalue of D'/?QD1/2