please refer to the screenshot

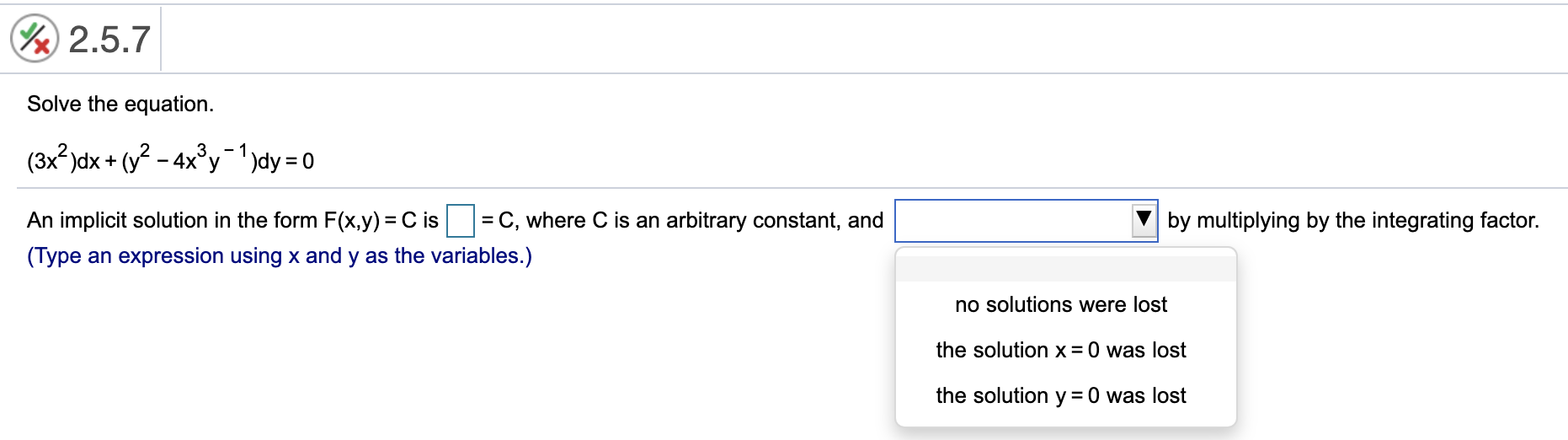
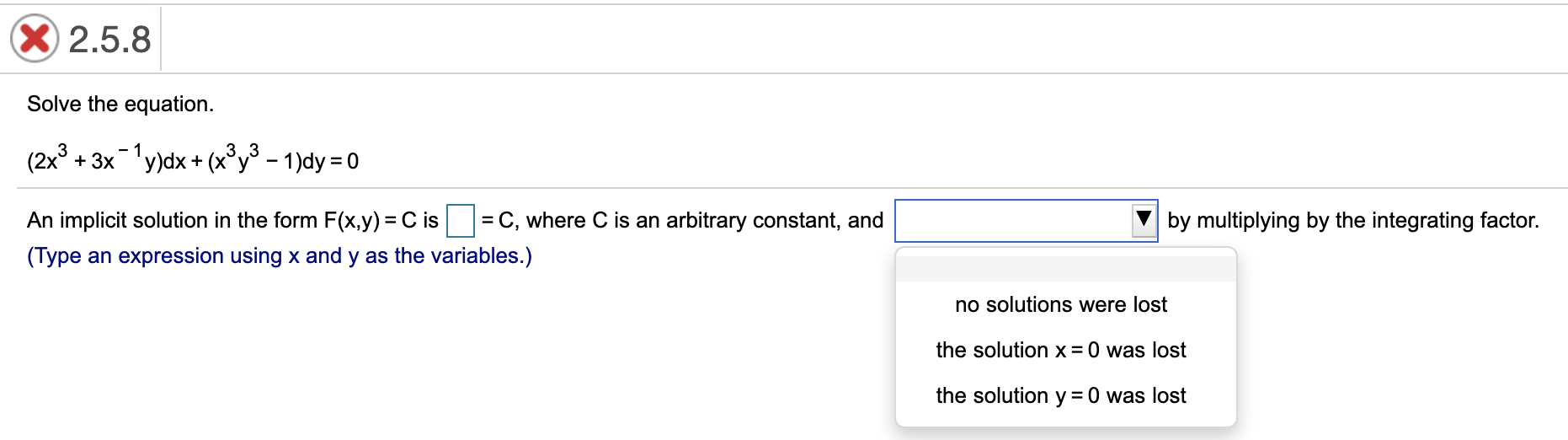
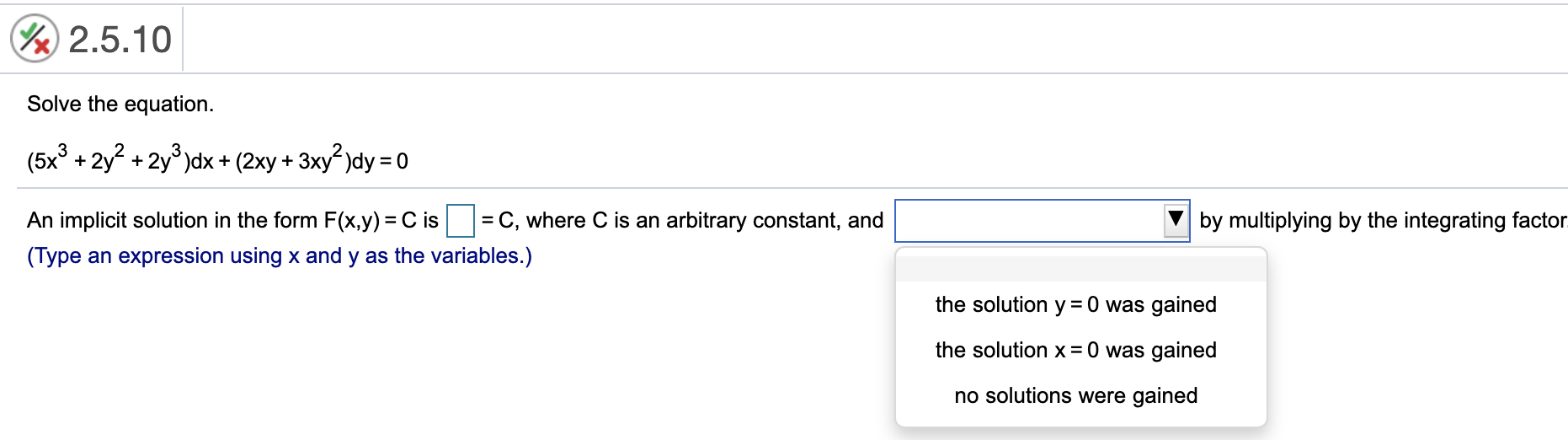
2.4.22 Solve the initial value problem. 3 3x 2y e 2Xy _ - dx + 2x e 2Xy + 2 dy = 0, y(2) = 1 K The solution is (Type an equation using x and y as the variables. Type an implicit solution.)@ 2.5.7 Solve the equation. (3x2)dx + (y2 4x3y '1)dy = 0 An implicit solution in the form F(x,y) = C is :l = C, where C is an arbitrary constant, and (Type an expression using x and y as the variables.) V by multiplying by the integrating factor. no solutions were lost the solution x =0 was lost the solution y =0 was lost 2.5.8 Solve the equation. (2x3 + 3x" 1y)dx + (x3y3 -1)dy = 0 An implicit solution in the form F(x,y) = C is :l = C, where C is an arbitrary constant, and (Type an expression using x and y as the variables.) V by multiplying by the integrating factor. no solutions were lost the solution x =0 was lost the solution y =0 was lost @2510 Solve the equation. (5x3 + 2y2 + 2y3)dx + (2xy + 3xy2)dy = 0 An implicit solution in the form F(x,y) = C is :l = C, where C is an arbitrary constant, and (Type an expression using x and y as the variables.) V by multiplying by the integrating factor the solution y = 0 was gained the solution x = 0 was gained no solutions were gained