Please run the following question in Matlab code

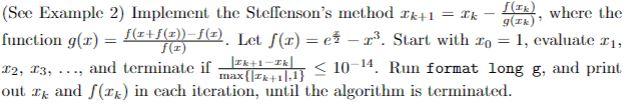
Below is the example the question wants referenced

Example 2: secant method for finding a zero of a nonlinear function f(x) % The algorithm is x_{k+1} = x_k - f(x_k)*(x_k-x_{k-1})/(f(x_k)-f(x_{k-1})) % % First we define the function f(x), then initialize x_0 and x_1. The first % step of the secand method gets x_2 = x_1-f(x_1)*(x_1-x_0)/(f(x_1)-f(x_0)) % the second step gets x_3 = x_2-f(x_2)*(x_2-x_1)/(f(x_2)-f(x_1)), etc. % This method is terminated when |x_{k+1}-x_k|/max(|x_{k+1}|,1)

% Define the function f(x) = (|x|^(1/2)+1)*cos(10*x)/exp(x/2)-x^4 in % *element-wise* operations (no need for sqrt(abs(x)).+1, 4.*x, and x./2) func = @(x)(sqrt(abs(x))+1).*cos(10*x)./exp(x/2)-x.^4; % initalize x0 = 0.3, x1 = 0.6 (what if we let x_0 = 0.7 and x_1 = 0.9?) x_initial = 0.3; xkm1 = x_initial; xk = 0.6; % maximum number of iterations we want to take maxiter = 100; % start the iteration of secant method for k = 1 : maxiter % the main computation of the algorithm xkp1 = xk - func(xk)*(xk-xkm1)/(func(xk)-func(xkm1)); % if x_{k+1} and x_k are sufficiently close, terminate the iteration if abs(xkp1-xk)/max([abs(xkp1) 1]) (See Example 2) Implement the Stellenson's method Ik+1 = Ik - f(x), where the g(IR) function g() = (x+(0))-f(a). Let S(I) = ei r? Start with 20 = 1, evaluate 11, 12, 13, and terminate il 2K+1-IR max{[+*+1,1)