Please see attachmetnt

Section 4.5: #14

Section 4.6: #12, #22, #36Section4.7:#10

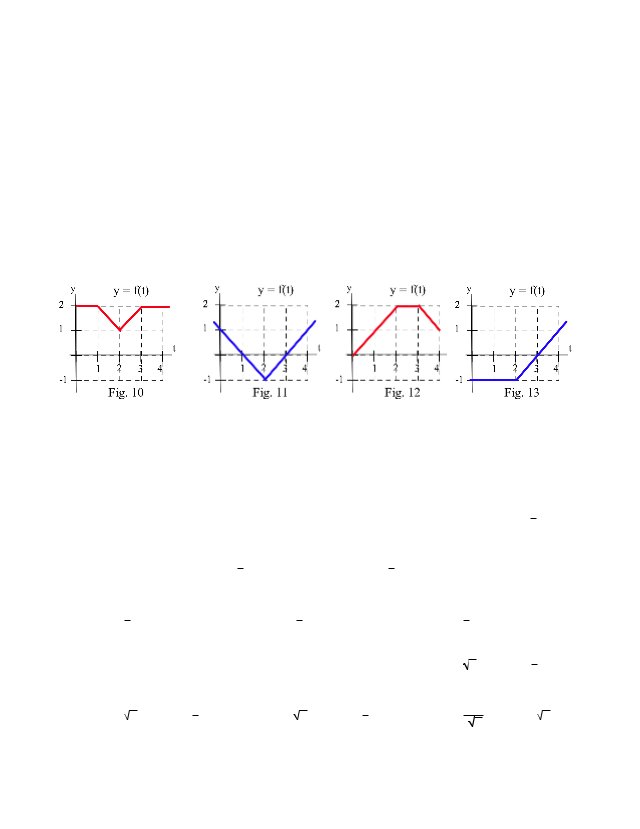
4.5 The Fundamental Theorem of Calculus Contemporary Calculus 9 In problems 3 - 8 , evaluate A'(x) at x = 1, 2, and 3. x x 3. A(x) = " ! 2t dt x 4. A(x) = " ! 2t dt 0 5. A(x) = " ! 2t dt 1 x -3 x 6. A(x) = " ! ( 3 - t 2) dt x 7. A(x) = " ! sin(t) dt 0 8. A(x) = " ! | t - 2 | dt 0 1 x In problems 9 - 13, A(x) = " ! f(t) dt for the functions in Figures 10 - 14. Evaluate A'(1), A'(2), A'(3). 0 9. f in Fig. 10 10. f in Fig. 11 11. f in Fig. 12 12. f in Fig. 13 In problems 13 - 33, verify that F(x) is an antiderivative of the integrand f(x) and use Part 2 of the Fundamental Theorem to evaluate the definite integrals. 4 1 13. " ! 2x dx , F(x) = x2 + 5 2 5 1 18. " ! x dx , F(x) = ln( x ) + 4 2 $/2 " cos(x) dx , F(x) = sin(x ) ! 0 4 ! x dx , F(x) = 23 x3/2 24. " 1 1 5 1 16. " ! (x + 4x - 3 ) dx , F(x) = 3 x3 + 2x2 - 3x 0 21. 3 ! x2 dx , F(x) = 13 x3 15. " 1 0 3 ! 3x2 dx , F(x) = x3 + 2 14. " 1 17. " ! x dx , F(x) = ln( x ) 1 3 1 19. " ! x dx , F(x) = ln( x ) 1/2 $ " sin(x) dx , F(x) = - cos(x) 22. ! 0 7 ! x dx , F(x) = 23 x3/2 25. " 1 3 1 20. " ! x dx , F(x) = ln( x ) + 2 1 1 23. " ! x dx , F(x) = 23 x3/2 0 4 1 26. " ! 2 x dx , F(x) = x 1 4.6 Finding Antiderivatives Contemporary Calculus 8 PROBLEMS 2 For problems 1 - 4, put f(x) = x , g(x) = x and verify that 2 1. 2 2 f(x) dx . g(x) dx f(x).g(x) dx 1 1 1 1 1 1 0 0 2. f(x).g(x) dx 3. f(x) dx . g(x) dx 0 2 2 1 1 4 4 1 1 f(x)/g(x) dx f(x) dx 2 / g(x) dx 1 4. f(x)/g(x) dx f(x) dx 4 / g(x) dx 1 For problems 5 - 14 , use the suggested u to find du and rewrite the integral in terms of u and du. Then find an antiderivative in terms of u , and, finally, rewrite your answer in terms of x . 5. cos(3x) dx u = 3x 6. sin(7x) dx u = 7x 7. ex sin(2 + ex ) dx u =2+e 8. e5x dx u = 5x 9. cos(x) sec2( sin(x) ) dx u = sin(x) 10. cos(x) sin(x) dx u = sin(x) 11. 3 +5 2x dx u = 3 + 2x 12. x2 (5 + x3 )7 dx u =5+x 13. x2 sin(1 + x3) dx u =1+x 3 14. x 3 x e x dx 1+e u =1+e x For problems 15 - 26 , use the change of variable technique to find an antiderivative in terms of x . 15. cos(4x) dx 16. e3x dx 17. x3 (5 + x4 )11 dx 18. x .sin( x2 ) dx 19. 2 3x 3 dx 20. sin(x) cos(x) dx 21. ln(x) dx x 22. x 1 - x2 dx 23. (1 + 3x ) 7 dx 24. 1x .sin( ln(x) ) dx 25. ex .sec(ex ).tan(ex ) dx 26. 1 cos( x ) dx 2+x x For problems 27 - 38 , evaluate the definite integrals. /2 27. cos( 3x ) dx 0 28. cos( 4x ) dx 0 1 x x 29. e .sin(2 + e ) dx 0 4.6 Finding Antiderivatives Contemporary Calculus 1 1 5x 30. e dx 1 2 35 31. x (1 + x ) dx 0 -1 2 ln(3) 5 33. 3 + 2x dx 4 5 10 32. x (x - 1) dx 0 34. 1 x e 2 35. x 1 - x dx x dx 0 1+e 0 5 0 1 2 36. 1 + x dx 1 37. 1 + 3x dx 2 39. 9 38. 0 2 sin (5x) dx 40. 0 2 cos (3x) dx 41. 1 2 2 - sin (x) dx 42. 1 dx 1 + 3x 3x 2 e + sin (x) dx 2 43. Find the area under one arch of the y = sin (x) graph. 2 44. Evaluate sin2(x) dx . 0 Problems 45 - 53 , expand the integrand and then find an antiderivative. 45. 2 3 (x +1) dx 46. 3 2 (x +5) dx 47. x 2 (e +1) dx 48. (x2 +3x - 2) 2 dx 49. (x2 +1)(x3 +5) dx 50. (7 + sin(x) ) 2 dx 51. ex (ex + e3x ) dx 52. (2 + sin(x) ) sin(x) dx 53. x (x2 +3x - 2) dx Problems 54 - 64 , perform the division and then find an antiderivative. 54. x + 1 dx x 56. 55. xx +- 12 dx 57. 2 xx +- 11 dx 58. 2 + 15 2x -x 13x dx -1 59. 2 + 18 2x -x 13x dx -1 60. 2 + 11 2x -x13x dx -1 61. xx +- 12 dx 62. x 3x e +xe 63. x + 4 dx 64. x x+ 3 dx e dx x+1 x 3x 1 = 1+x ) ( x x+1 dx 3x ( x+1 3 = 3 - x+1 ) 4.7 Applications of Integration Contemporary Calculus 7 In the previous Example and Practice problem, the force was variable and the distance was "x. In later sections we will examine situations where the force is constant and the distance changes. Summary These area, average and work applications simply introduce a few of the applications of definite integrals and illustrate the pattern of going from an applied problem to a Riemann sum, on to a definite integral and, finally, to a number. More applications will be explored in Chapter 5. The rest of this chapter will examine additional ways of finding antiderivatives and of finding the values of definite integrals when an antiderivative can not be found. PROBLEMS In problems 1 - 4, use the values in Table 1 to estimate the areas. 1. Estimate the area between f and g for 1 $ x $ 4. 2. Estimate the area between f and g for 1 $ x $ 6. 3. Estimate the area between f and h for 0 $ x $ 4. 4. Estimate the area between g and h for 0 $ x $ 6. 5. Estimate the area of the island in Fig. 13. 6. Estimate the area of the island in Fig. 13 if the distances x! f(x)! 0! 1! 2! 3! 4! 5! 6! 5! 6! 6! 4! 3! 2! 2! g(x)! h(x)"" 2! 1! 2! 2! 3! 4! 5! 5 6 8 6 5 4 2 Table 1 between the lines is 50 feet instead of 40 feet,. In problems 7 - 18, sketch the graph of each function and find the area between the graphs of f and g for x in the given interval. 7. 2 f(x) = x + 3 , g(x) = 1 and -1 $ x $ 2. 8. 2 f(x) = x + 3 , g(x) = 1 + x and 0 $ x $ 3. 9. 2 f(x) = x , g(x) = x and 0 $ x $ 2. 10. f(x) = 4 - x 2 , g(x) = x + 2 and 0 $ x $ 2. 1 11. f(x) = x , g(x) = x and 1 $ x $ e. 12. f(x) = x , g(x) = x and 0 $ x $ 4. 13. f(x) = x + 1 , g(x) = cos(x ) and 0 $ x $ /4. 2 14. f(x) = (x -1) , g(x) = x + 1 and 0 $ x $ 3. x 15. f(x) = e , g(x) = x and 0 $ x $ 2. 16. f(x) = cos(x ), g(x) = sin(x ) and 0 $ x $ /4