please see the attachments

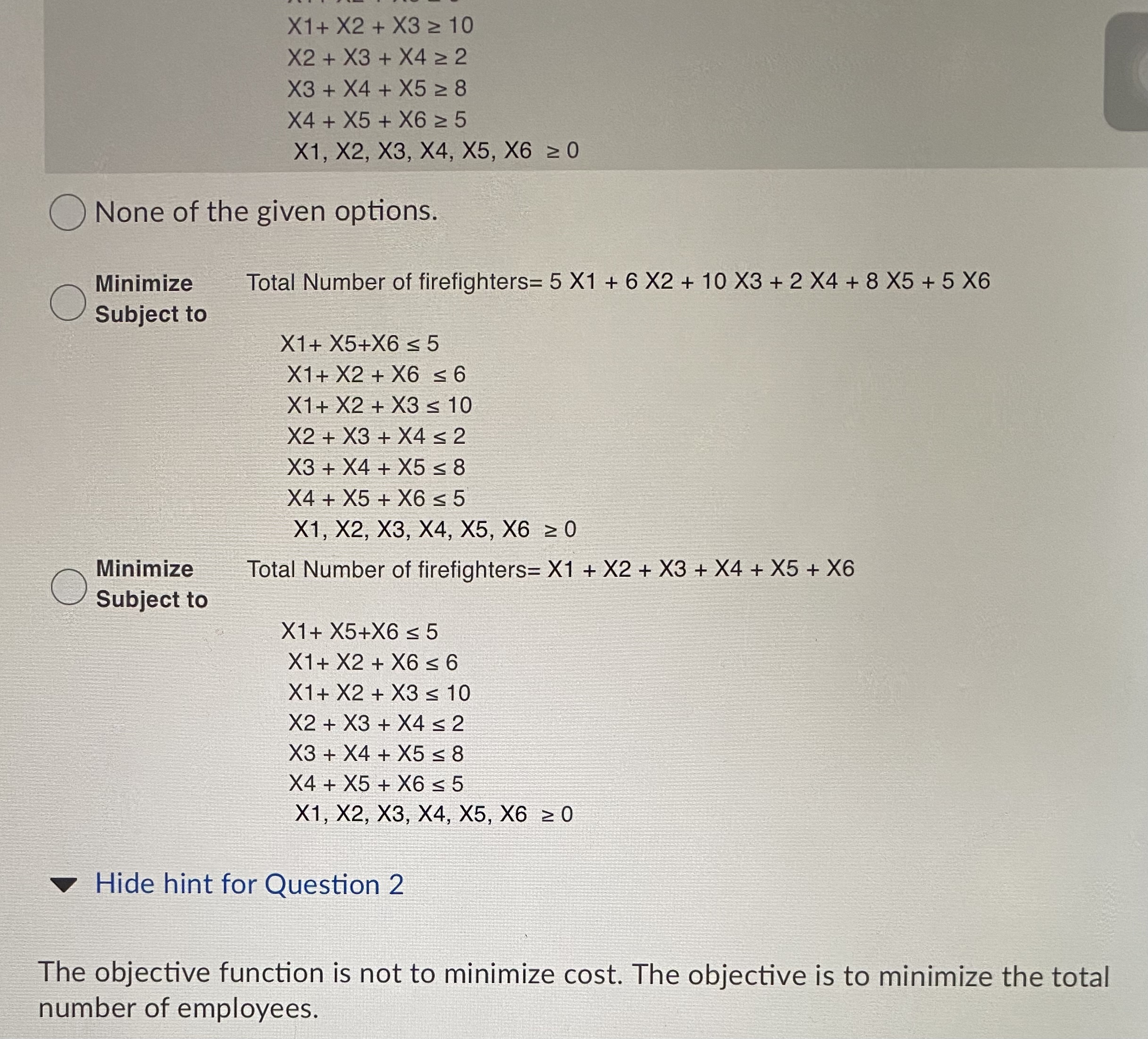
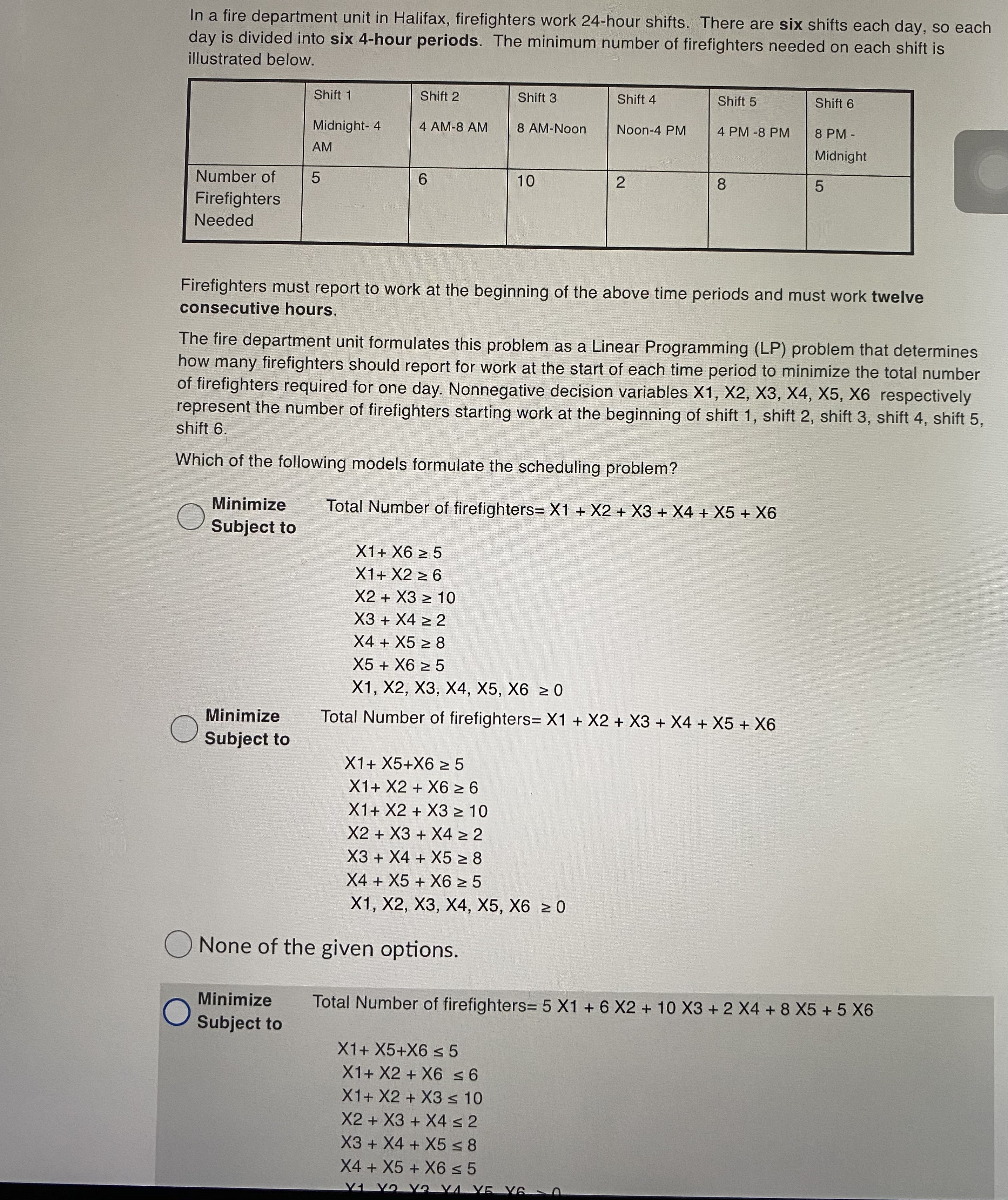
X1+ X2 + X3 > 10 X2 + X3 + X4 > 2 X3 + X4 + X5 2 8 X4 + X5 + X6 2 5 X1, X2, X3, X4, X5, X6 2 0 ONone of the given options. Minimize Total Number of firefighters= 5 X1 + 6 X2 + 10 X3 + 2 X4 + 8 X5 + 5 X6 Subject to X1+ X5+X6 s 5 X1+ X2 + X6 = 6 X1+ X2 + X3 s 10 X2 + X3 + X4 s 2 X3 + X4 + X5 s 8 X4 + X5 + X6 s 5 X1, X2, X3, X4, X5, X6 2 0 Minimize Total Number of firefighters= X1 + X2 + X3 + X4 + X5 + X6 Subject to X1 + X5+X6 s 5 X1+ X2 + X6 s 6 X1 + X2 + X3 s 10 X2 + X3 + X4 s 2 X3 + X4 + X5 s 8 X4 + X5 + X6 s 5 X1, X2, X3, X4, X5, X6 2 0 Hide hint for Question 2 The objective function is not to minimize cost. The objective is to minimize the total number of employees.In a fire department unit in Halifax, firefighters work 24-hour shifts. There are six shifts each day, so each day is divided into six 4-hour periods. The minimum number of firefighters needed on each shift is illustrated below. Shift 1 Shift 2 Shift 3 Shift 4 Shift 5 Shift 6 Midnight- 4 4 AM-8 AM 8 AM-Noon Noon-4 PM 4 PM -8 PM 8 PM - AM Midnight Number of 5 6 10 2 8 Firefighters Needed Firefighters must report to work at the beginning of the above time periods and must work twelve consecutive hours. The fire department unit formulates this problem as a Linear Programming (LP) problem that determines how many firefighters should report for work at the start of each time period to minimize the total number of firefighters required for one day. Nonnegative decision variables X1, X2, X3, X4, X5, X6 respectively represent the number of firefighters starting work at the beginning of shift 1, shift 2, shift 3, shift 4, shift 5, shift 6 Which of the following models formulate the scheduling problem? Minimize Total Number of firefighters= X1 + X2 + X3 + X4 + X5 + X6 Subject to X1+ X6 2 5 X1 + X2 2 6 X2 + X3 2 10 X3 + X4 2 2 X4 + X5 2 8 X5 + X6 2 5 X1, X2, X3, X4, X5, X6 2 0 Minimize Total Number of firefighters= X1 + X2 + X3 + X4 + X5 + X6 O Subject to X1+ X5+X6 2 5 X1 + X2 + X6 2 6 X1+ X2 + X3 2 10 X2 + X3 + X4 2 2 X3 + X4 + X5 2 8 X4 + X5 + X6 2 5 X1, X2, X3, X4, X5, X6 2 0 ONone of the given options. Minimize Total Number of firefighters= 5 X1 + 6 X2 + 10 X3 + 2 X4 + 8 X5 + 5 X6 Subject to X1+ X5+X6 s 5 X1+ X2 + X6 s 6 X1+ X2 + X3 s 10 X2 + X3 + X4 s 2 X3 + X4 + X5 s 8 X4 + X5 + X6 s 5 y1 yo ya YA Y5 Y6