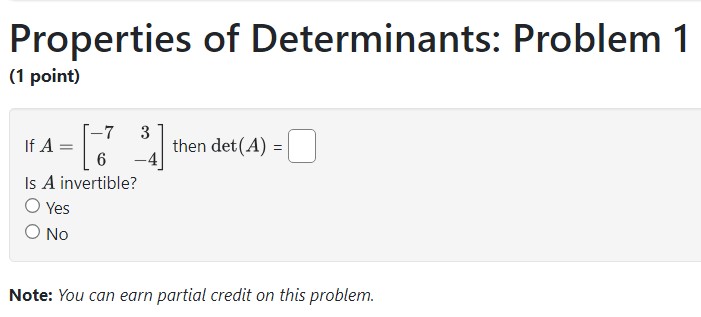
Please show all work so I can understand these problems and box all answers.

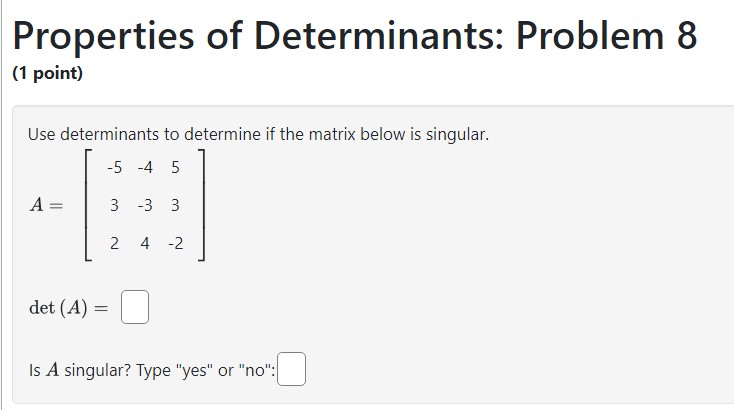
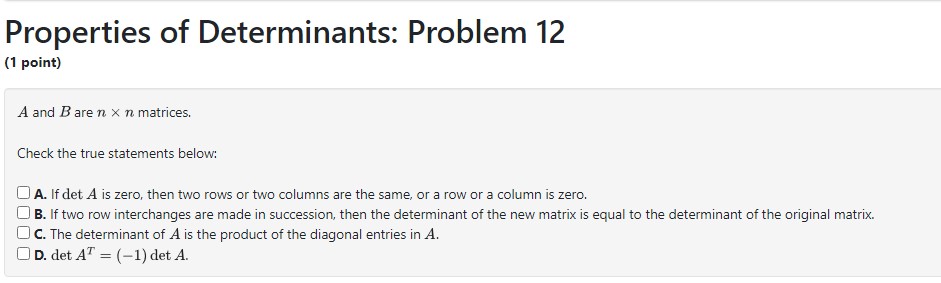
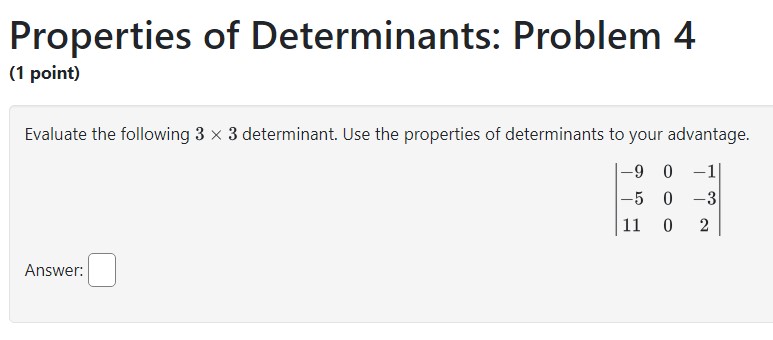
Properties of Determinants: Problem 1 (1 point) -7 3 B If A= { 6 _4} then det(A) = |_| Is A invertible? O Yes O No Note: You can earn partial credit on this problem. \fProperties of Determinants: Problem 11 (1 point) If A and B are 4 x 4 matrices, det (A) = -2, det (B) = 8, then det ( AB) = det(2A) = det (AT) = det ( B-]) = det ( B)) =Properties of Determinants: Problem 12 (1 point) A and B are n x n matrices. Check the true statements below: [J A. If det A is zero, then two rows or two columns are the same, or a row or a column is zera, () B. If two row interchanges are made in succession, then the determinant of the new matrix is equal to the determinant of the original matrix. () . The determinant of A is the product of the diagonal entries in A. (I D. det AT = (1)det A. \f\fProperties of Determinants: Problem 4 (1 point) Evaluate the following 3 x 3 determinant. Use the properties of determinants to your advantage. -8 0 1 -5 0 -3 11 0 2 Answer: | | Properties of Determinants: Problem 5 (1 point) The determinant of the matrix -2 -7 -9 -7 A 0 3 -8 -9 is| | Hint: Find a good row or column and expand by minors. e o o o = e Properties of Determinants: Problem 6 (1 point) The determinant of the matrix A = is Hint: Find a good row or column and expand by minors.Properties of Determinants: Problem 7 (1 point) The determinant of the matrix 2 -J 1 3 4 5 6 8 1 2 3 4 5 6 7 8 1 2 3 4 6 8 A = 3 5 6 N 2 3 6 7 8 1 2 3 4 5 6 7 8 -J 9 1 2 3 4 5 6 8 4 5 6 -J 2 8 is Hint: Remember that a square linear system has a unique solution if the determinant of the coefficient matrix is non-zero.Properties of Determinants: Problem 8 (1 point) Use determinants to determine if the matrix below is singular. 5 -4 5 A= 2 e 2 4 2 det (4) = | | Is A singular? Type "yes" or "no": | Properties of Determinants: Problem 9 {1 point) Use determinants to determine whether each of the following sets of vectors is linearly dependent or independent. Select an Answer v 1 3 = -3 i 1 at 7 2 _'1 4 _5 2 2 -3 0 3 Select an Answer v | 2. 2 -4 4 2 =3 3 0 - 1 ' J -1 ' 30 ! 3 -10 10 20 Select an Answer v 3 1 5 3 -3 : -1 : 5 : _"I 2 4 Select an Answer v 4 - -16 -24 -3 -18 -26 4 19 25