Please show calculations and explain so I can understand how to solve these types of problems.

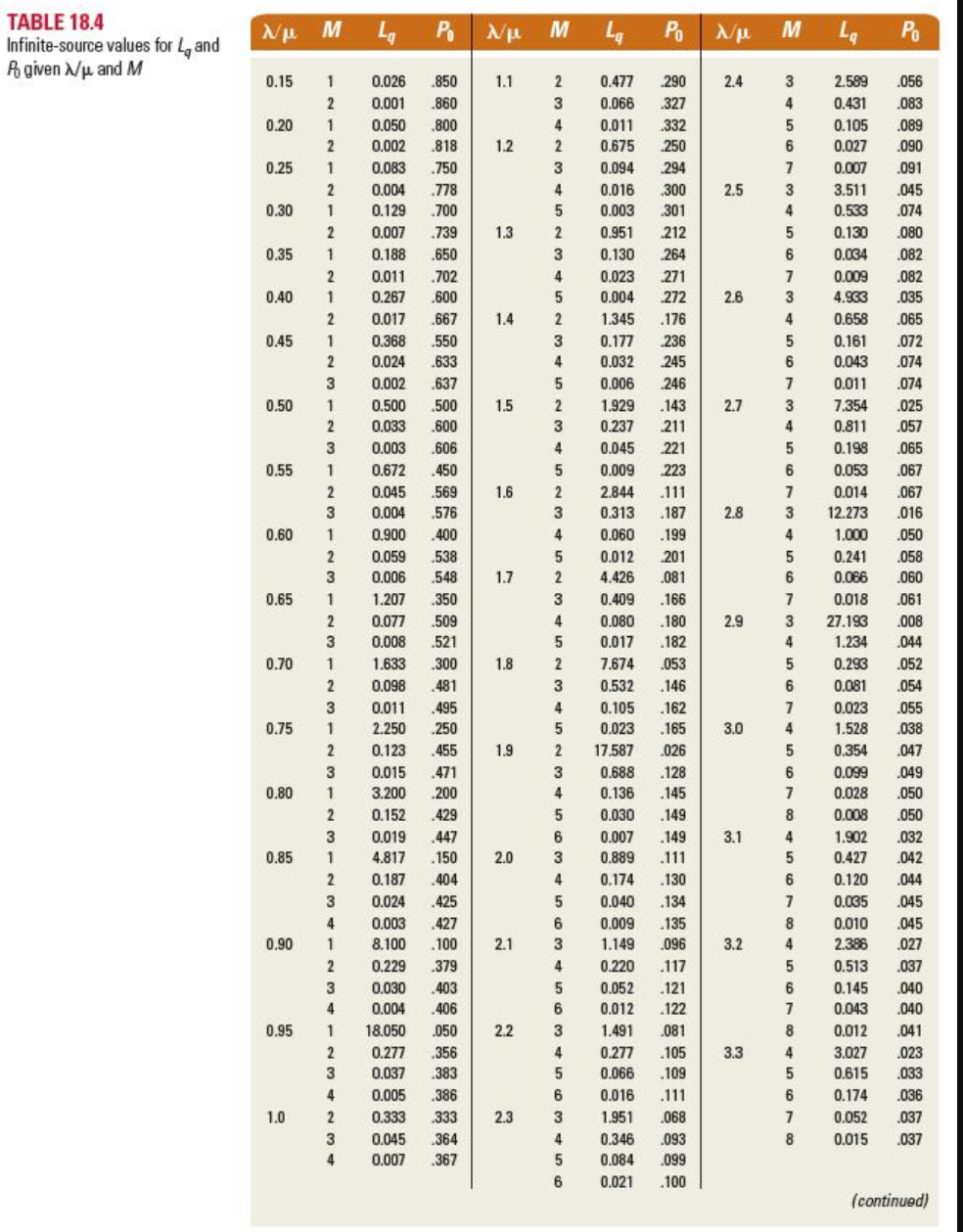
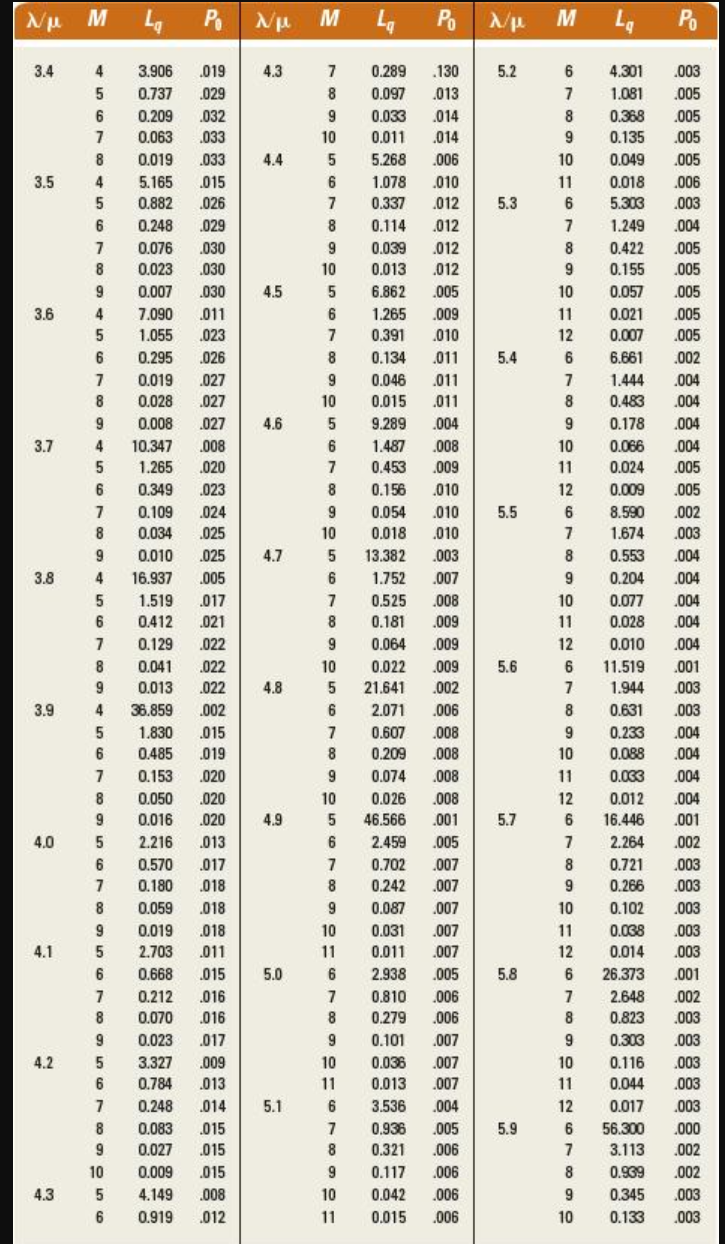
The manager of a regional warehouse must decide on the number of loading docks to request for a new facility in order to minimize the sum of dock costs and driver-truck costs. The manager has learned that each driver-truck combination represents a cost of $300 per day and that each dock plus loading crew represents a cost of $1,100 per day. Use Table 1 and Table 2. a. How many docks should be requested if trucks arrive at the rate of three per day, each dock can handle five trucks per day, and both rates are Poisson? b. An employee has proposed adding new equipment that would speed up the loading rate to 6 trucks per day. The equipment would cost an additional $100 per day for each dock. Should the manager invest in the new equipment? (Round your cost amount to 2 decimal places and all other calculations to 3 decimal places.) , because the daily total cost with the new equipment is $ which is lower than without the new equipment. TABLE 18.4 Infinite-source values for Lq and B0 given / and M \begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline & M & Lq & P0 & N & M & Lq & P0 & / & M & Lq & P0 \\ \hline \multirow[t]{5}{*}{3.4} & 4 & 3.906 & .019 & 4.3 & 7 & 0.289 & .130 & \multirow[t]{6}{*}{5.2} & 6 & 4.301 & .003 \\ \hline & 5 & 0.737 & .029 & & 8 & 0.097 & .013 & & 7 & 1.081 & .005 \\ \hline & 6 & 0.209 & .032 & & 9 & 0.033 & .014 & & 8 & 0.368 & .005 \\ \hline & 7 & 0.063 & .033 & & 10 & 0.011 & .014 & & 9 & 0.135 & .005 \\ \hline & 8 & 0.019 & .033 & 4.4 & 5 & 5.268 & .006 & & 10 & 0.049 & .005 \\ \hline \multirow[t]{6}{*}{3.5} & 4 & 5.165 & .015 & & 6 & 1.078 & .010 & & 11 & 0.018 & .006 \\ \hline & 5 & 0.882 & .026 & & 7 & 0.337 & .012 & \multirow[t]{7}{*}{5.3} & 6 & 5.300 & .003 \\ \hline & 6 & 0.248 & .029 & & 8 & 0.114 & .012 & & 7 & 1.249 & .004 \\ \hline & 7 & 0.076 & .030 & & 9 & 0.039 & .012 & & 8 & 0.422 & .005 \\ \hline & 8 & 0.023 & .030 & & 10 & 0.013 & .012 & & 9 & 0.155 & .005 \\ \hline & 9 & 0.007 & .030 & 4.5 & 5 & 6.862 & .005 & & 10 & 0.057 & .005 \\ \hline \multirow[t]{6}{*}{3.6} & 4 & 7.090 & .011 & & 6 & 1.265 & .009 & & 11 & 0.021 & .005 \\ \hline & 5 & 1.055 & .023 & & 7 & 0.391 & .010 & & 12 & 0.007 & .005 \\ \hline & 6 & 0.295 & .026 & & 8 & 0.134 & .011 & \multirow[t]{7}{*}{5.4} & 6 & 6.661 & .002 \\ \hline & 7 & 0.019 & .027 & & 9 & 0.046 & .011 & & 7 & 1.444 & .004 \\ \hline & 8 & 0.028 & .027 & & 10 & 0.015 & .011 & & 8 & 0.483 & .004 \\ \hline & 9 & 0.008 & .027 & 4.6 & 5 & 9.289 & .004 & & 9 & 0.178 & .004 \\ \hline \multirow[t]{6}{*}{3.7} & 4 & 10.347 & .008 & & 6 & 1.487 & .008 & & 10 & 0.066 & .004 \\ \hline & 5 & 1.265 & .020 & & 7 & 0.453 & .009 & & 11 & 0.024 & .005 \\ \hline & 6 & 0.349 & .023 & & 8 & 0.156 & .010 & & 12 & 0.009 & .005 \\ \hline & 7 & 0.109 & .024 & & 9 & 0.054 & .010 & \multirow[t]{7}{*}{5.5} & 6 & 8.590 & .002 \\ \hline & 8 & 0.034 & .025 & & 10 & 0.018 & .010 & & 7 & 1.674 & .003 \\ \hline & 9 & 0.010 & .025 & 4.7 & 5 & 13.382 & .003 & & 8 & 0.553 & .004 \\ \hline \multirow[t]{6}{*}{3.8} & 4 & 16.937 & .005 & & 6 & 1.752 & .007 & & 9 & 0.204 & .004 \\ \hline & 5 & 1.519 & .017 & & 7 & 0.525 & .008 & & 10 & 0.077 & .004 \\ \hline & 6 & 0.412 & .021 & & 8 & 0.181 & .009 & & 11 & 0.028 & .004 \\ \hline & 7 & 0.129 & .022 & & 9 & 0.064 & .009 & & 12 & 0.010 & .004 \\ \hline & 8 & 0.041 & .022 & & 10 & 0.022 & .009 & \multirow[t]{7}{*}{5.6} & 6 & 11.519 & .001 \\ \hline & 9 & 0.013 & .022 & 4.8 & 5 & 21.641 & .002 & & 7 & 1.944 & .003 \\ \hline \multirow[t]{6}{*}{3.9} & 4 & 36.859 & .002 & & 6 & 2.071 & .006 & & 8 & 0.631 & .003 \\ \hline & 5 & 1.830 & .015 & & 7 & 0.607 & .008 & & 9 & 0.233 & .004 \\ \hline & 6 & 0.485 & .019 & & 8 & 0.209 & .008 & & 10 & 0.088 & .004 \\ \hline & 7 & 0.153 & .020 & & 9 & 0.074 & .008 & & 11 & 0.033 & .004 \\ \hline & 8 & 0.050 & .020 & & 10 & 0.026 & .008 & & 12 & 0.012 & .004 \\ \hline & 9 & 0.016 & .020 & 4.9 & 5 & 46.566 & .001 & \multirow[t]{7}{*}{5.7} & 6 & 16.446 & .001 \\ \hline \multirow[t]{5}{*}{4.0} & 5 & 2.216 & .013 & & 6 & 2.459 & .005 & & 7 & 2.264 & .002 \\ \hline & 6 & 0.570 & .017 & & 7 & 0.702 & .007 & & 8 & 0.721 & .003 \\ \hline & 7 & 0.180 & .018 & & 8 & 0.242 & .007 & & 9 & 0.266 & .003 \\ \hline & 8 & 0.059 & .018 & & 9 & 0.087 & .007 & & 10 & 0.102 & .003 \\ \hline & 9 & 0.019 & .018 & & 10 & 0.031 & .007 & & 11 & 0.038 & .003 \\ \hline \multirow[t]{5}{*}{4.1} & 5 & 2.703 & .011 & & 11 & 0.011 & .007 & & 12 & 0.014 & .003 \\ \hline & 6 & 0.668 & .015 & 5.0 & 6 & 2.938 & .005 & \multirow[t]{7}{*}{5.8} & 6 & 26.373 & .001 \\ \hline & 7 & 0.212 & .016 & & 7 & 0.810 & .006 & & 7 & 2.648 & .002 \\ \hline & 8 & 0.070 & .016 & & 8 & 0.279 & .006 & & 8 & 0.823 & .003 \\ \hline & 9 & 0.023 & .017 & & 9 & 0.101 & .007 & & 9 & 0.303 & .003 \\ \hline \multirow[t]{6}{*}{4.2} & 5 & 3.327 & .009 & & 10 & 0.036 & .007 & & 10 & 0.116 & .003 \\ \hline & 6 & 0.784 & .013 & & 11 & 0.013 & .007 & & 11 & 0.044 & .003 \\ \hline & 7 & 0.248 & .014 & 5.1 & 6 & 3.536 & .004 & & 12 & 0.017 & .003 \\ \hline & 8 & 0.083 & .015 & & 7 & 0.936 & .005 & 5.9 & 6 & 56.300 & .000 \\ \hline & 9 & 0.027 & .015 & & 8 & 0.321 & .006 & & 7 & 3.113 & .002 \\ \hline & 10 & 0.009 & .015 & & 9 & 0.117 & .006 & & 8 & 0.969 & .002 \\ \hline 4.3 & 5 & 4.149 & .008 & & 10 & 0.042 & .006 & & 9 & 0.345 & .003 \\ \hline & 6 & 0.919 & .012 & & 11 & 0.015 & .006 & & 10 & 0.133 & .003 \\ \hline \end{tabular}