Please show how to use the finite difference method to find the solution of two partial differential equations (continuity and momentum) for the height of the fluid h and its velocity u, both of which depend on position x and time t. Please show all the steps!

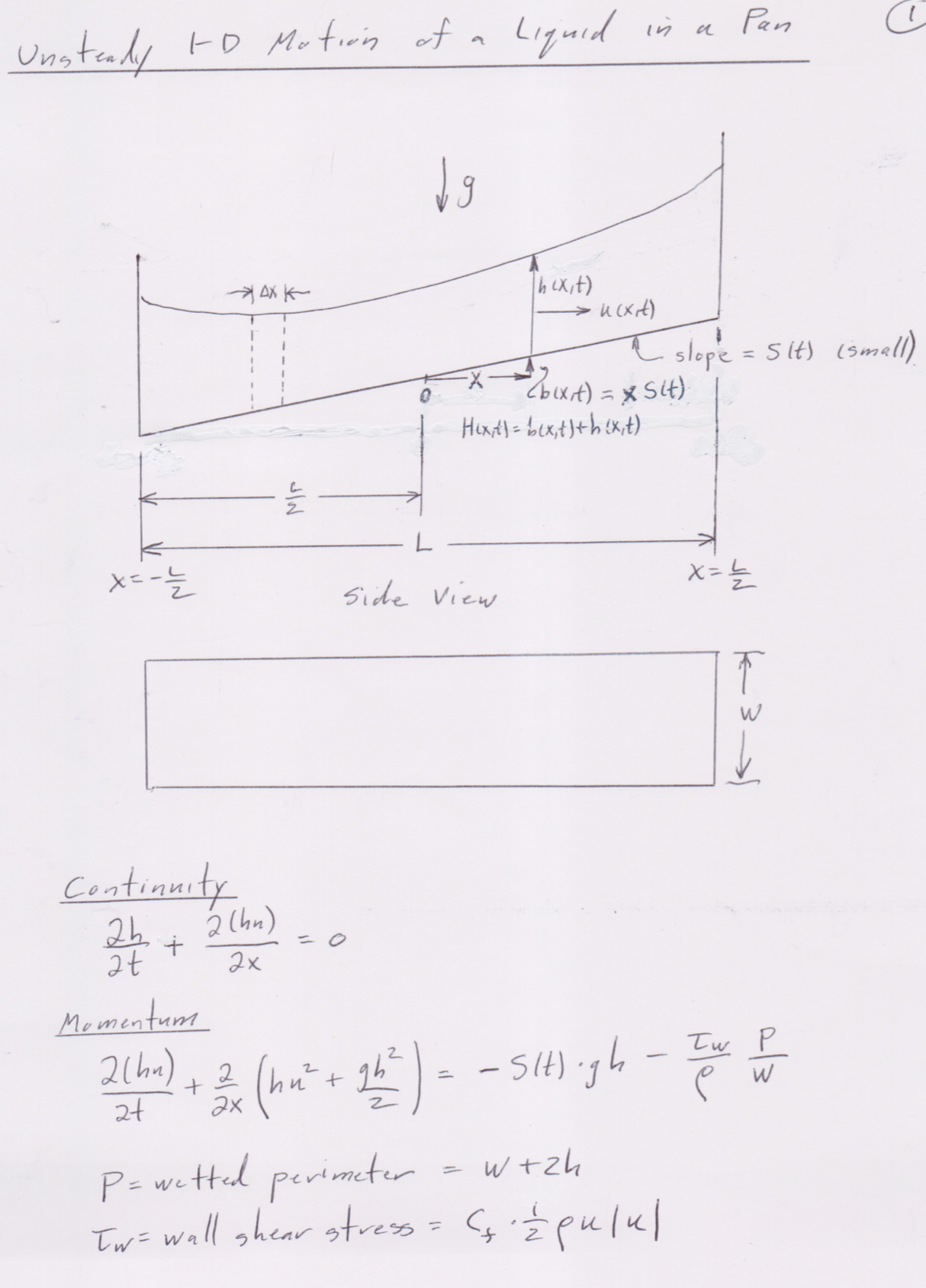
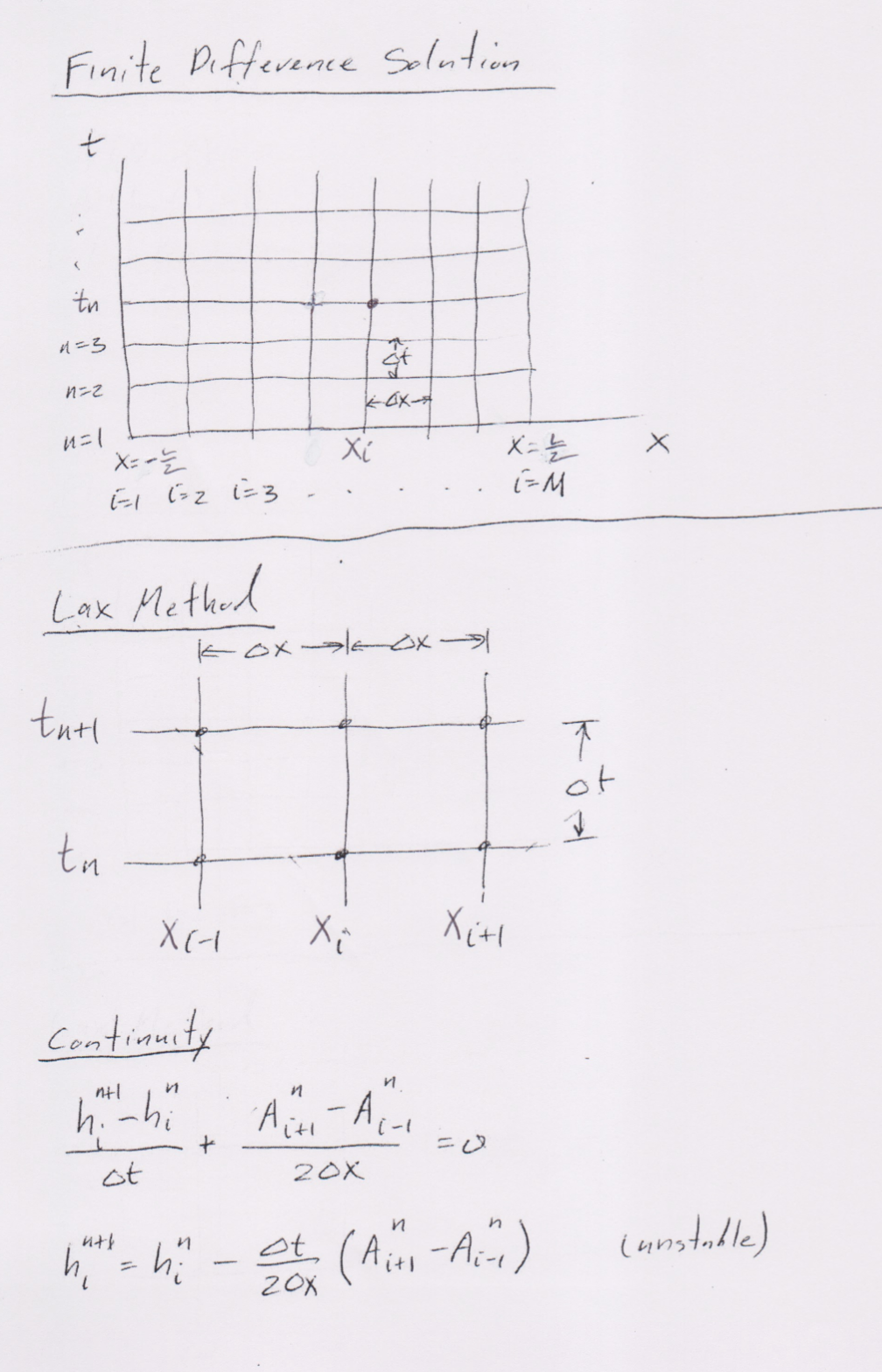
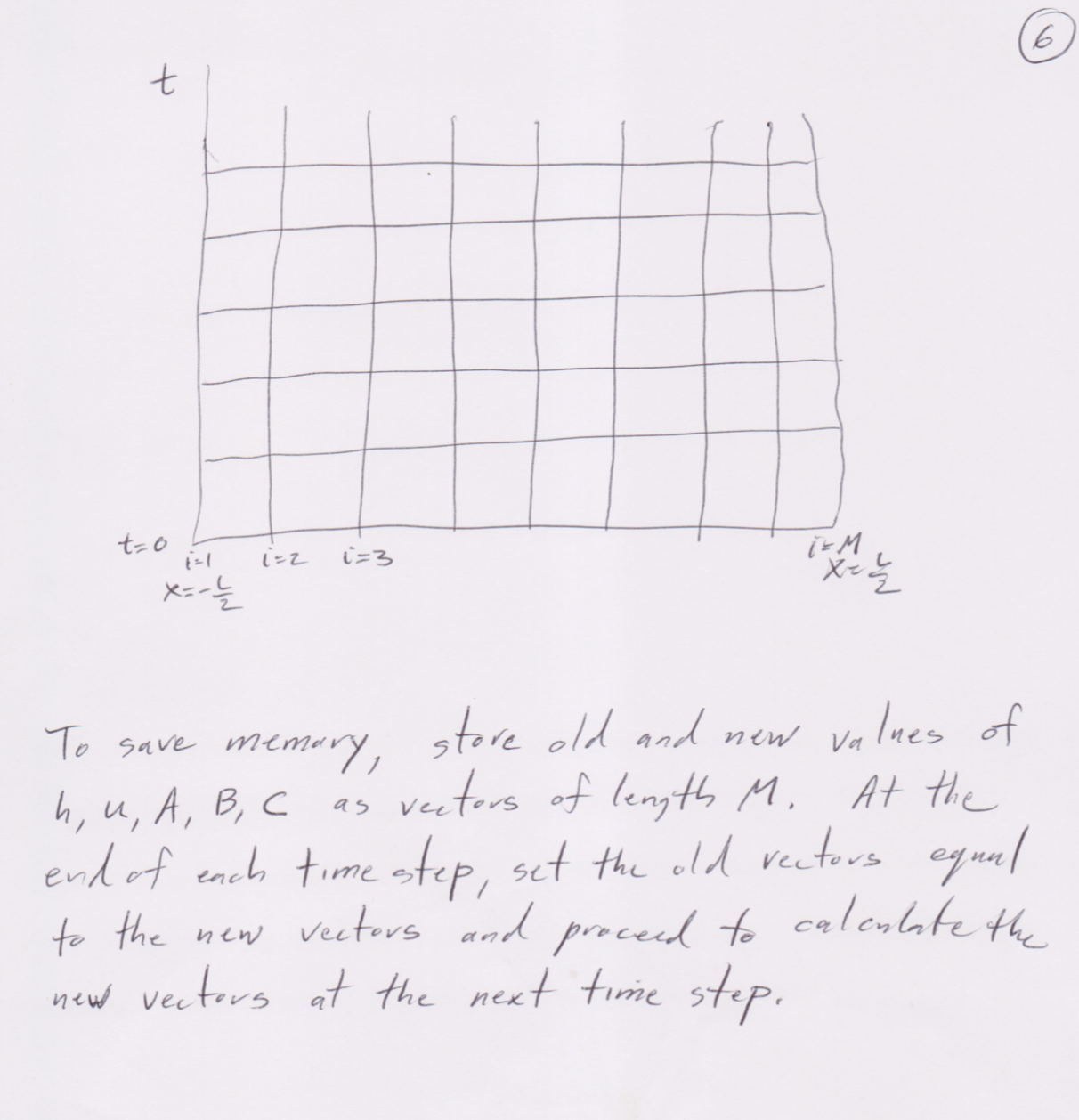
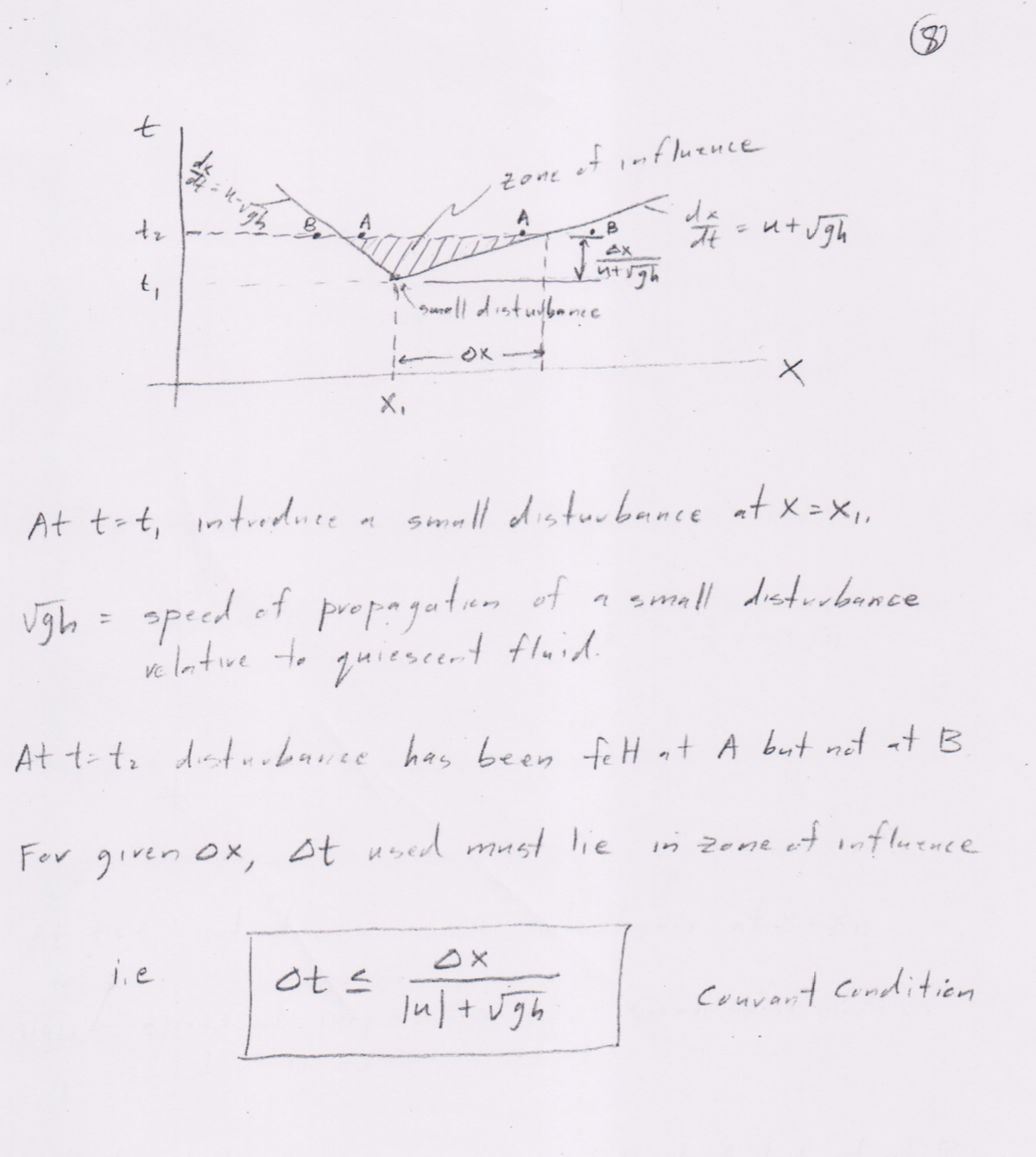
Unsteady 10 Motion of a Liquid in a Pan 19 -XAX K hexit ) > u (xit ) A slope = 5 It) ( small ) Hexitl = bex, + ) + hex,t ) L Side View W Continuity 26 2 ( hn ) 2t 2x = 0 Momentum 2 ( hn ) + 2 2x ( hurt gb = - Sit high - Iw p W P= wetted perimeter = w tzh Tw = wall shear stress = Cy.z pululBoundary Conditions " (# , t ) = 0 u liz, t ) = 0 Initial Conditions h ( x 1 0 ) = ho u ( x, 0 ) = 0 Define A = hu B = hu2 + 9 62 2 C = - Sttigh + Csulu) ( 8) ] Equations become 2h + 2A = at 2x ( continuity ) 2A- 2B = C ( momentum) at 2x Boundary Conditions Ate It ) = 0 A ( z , t ) = 0 Initial Conditions hex,0) = 17. Acx, 0) = 0Finite Difference Solution + tn 1 = 3 St K OX - X= - 2 Xi X 1=1 1=2 1=3 1 = M Lax Method KOX -60x-1 tutl of tn V Xi Xitl continuity h. - hi + at 20X h , " = h , " ot ( Aiti - Ac-. ) 20X ( unstable )In the Lax method, hi is replaced bay hi = = (hit the. ) hi = = ( hit, this, ) - st ( Ant , - A?. )1 conditionally ) stable Similarly for Momentum Ai = = ( Altit Air, ) - - ot (Biti - Bird ) + = ( City + C ) ot 20 x U." is calculated from AiAt left wall (i=1 ) 5 To satinty new at x=- u 5 ( ( ) s ( t ) U. = - Uz 1-1 1=2 n = h , This gives A . " = - Az " Co :- C z n For i = 1 - Ac n+1 h = ich, + ho - of 20X ( AL " - A . " ) OX not! = 0 ) A, ( since u , obtain similar expressions too right wall6 t t=0 1=1 1=2 1= 3 X=- C Xug To save memary , store old and new values of h, u, A, B, C as vectors of length M. At the end of each time step, set the old vectors equal to the new vectors and proceed to calculate the new vectors at the next time step.Suggested values L = 1 m ho = 0.1 m W = 0. 25 m (s = 0.005 Ox = 0.01 m Do the following runs 1) SIt ) = 0. 1 (constant ) (t20 ) 2 ) SIt ) = Ol sinwt (tz0 ) observe what happens for different values of w.ak zone of influence A AX t , butugh 1 smell disturbance X, X At tat, Introduce a small disturbance at x= x,. Ugh = speed of propagation of a small disturbance relative to quiescent fluid. At titz disturbance has been fell at A but not at B For given Ox, At used must lie in zone of influence ots OX In +ugh Courant Condition