Please show steps on how to solve:

Student's t-distribution - THE VERY EXPENSIVE SHOE COMPANY

Formulas:

Let xbar = The sample mean of the population you are trying to determine (?x / n).

Let = The true mean of the population you are trying to determine. For this type of problem, we will set equal to the xbar and find the confidence interval (CI) around it.

The transformation formula for comparing a sample mean to the population mean and using the Student's t-distribution:

t =(xbar - ) / ?x where ?x = S / ? n so by extension t = (xbar - ) ? n / S

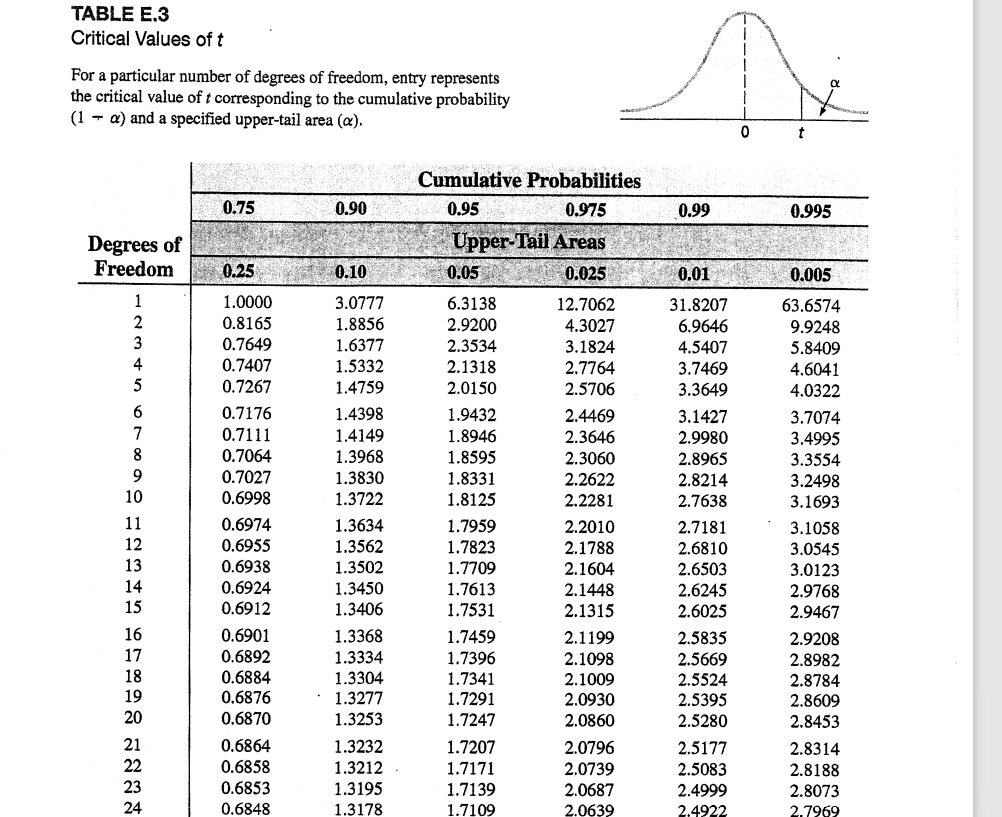
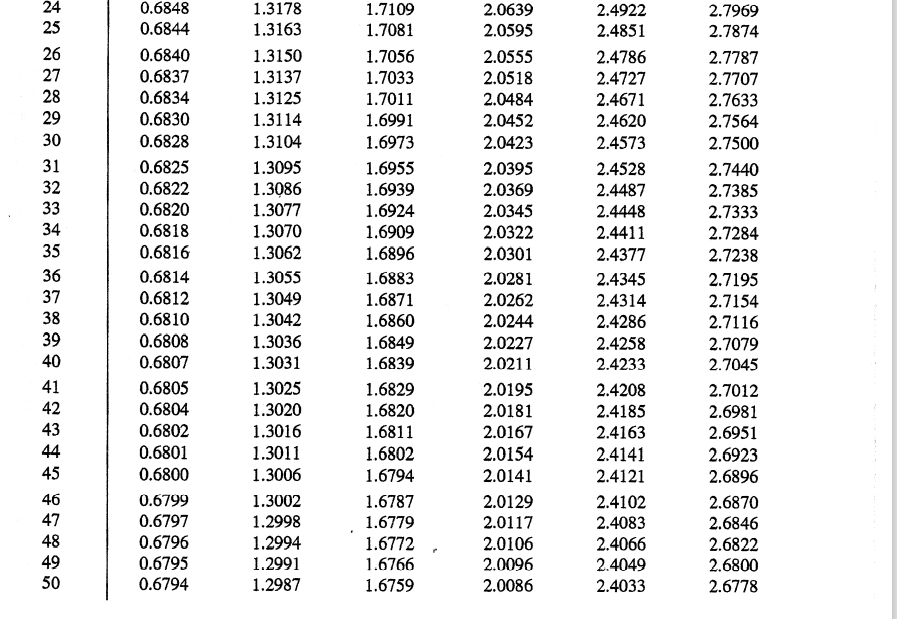
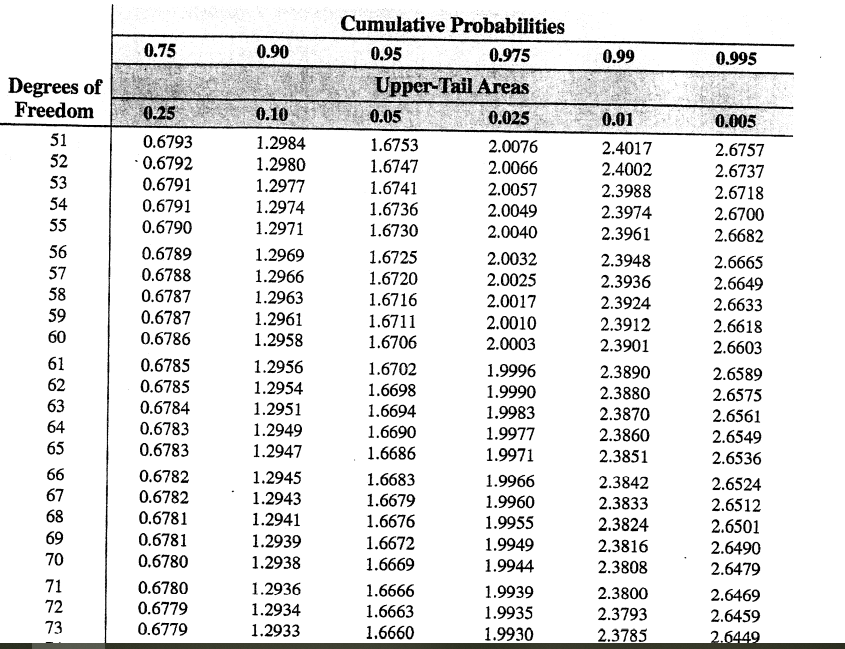
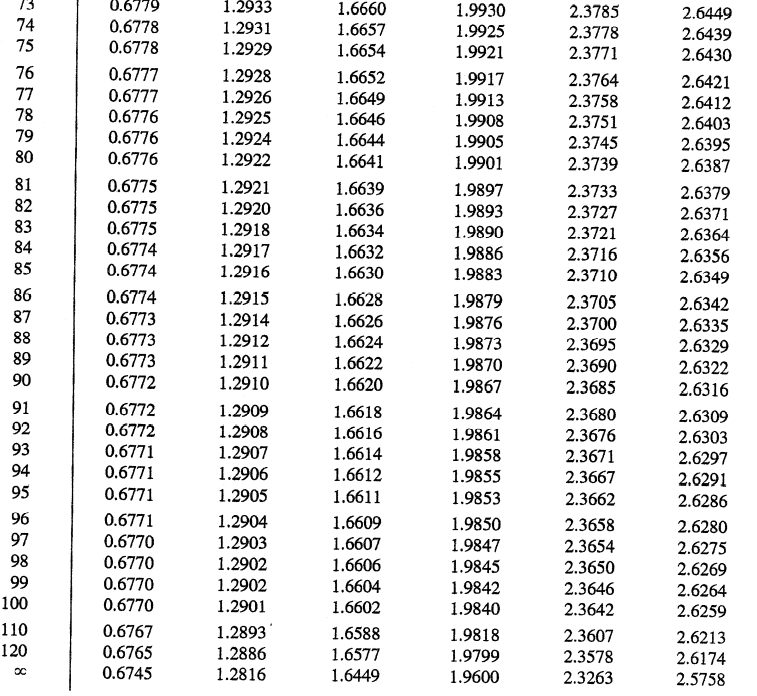
Reading the table for Student's t-distribution:

Degrees of Freedom (DOF) means that if you know xbar already, then it is the number of x values that you need to know before the remainder can be determined. For this problem, DOF = n - 1.

The first column represents the degrees of freedom and the remaining columns represent different probabilities. For example, if you are trying to determine the +/- t-score for a 95% CI then you should use the .0250 column as that will give you the absolute value of the t-score.

Example: The Very Expensive Shoe Company

Suppose a sample of 64 sales invoices is selected from the population of sales invoices during the month and the sample mean of the 64 sales invoices is $110.27, with a sample standard deviation of $28.95. What would be the interval if the company requires 95% CI?

{ Please use the t table and present your answer to two decimal places, ex. [$65.81, $154.73] }

\f\f\f\f