Question: please show work/steps clearly Evaluate the given limits. Exercise 1. [1 mark] x - 7 lim x-7 X Exercise 2. [3 marks] 2x2 - x
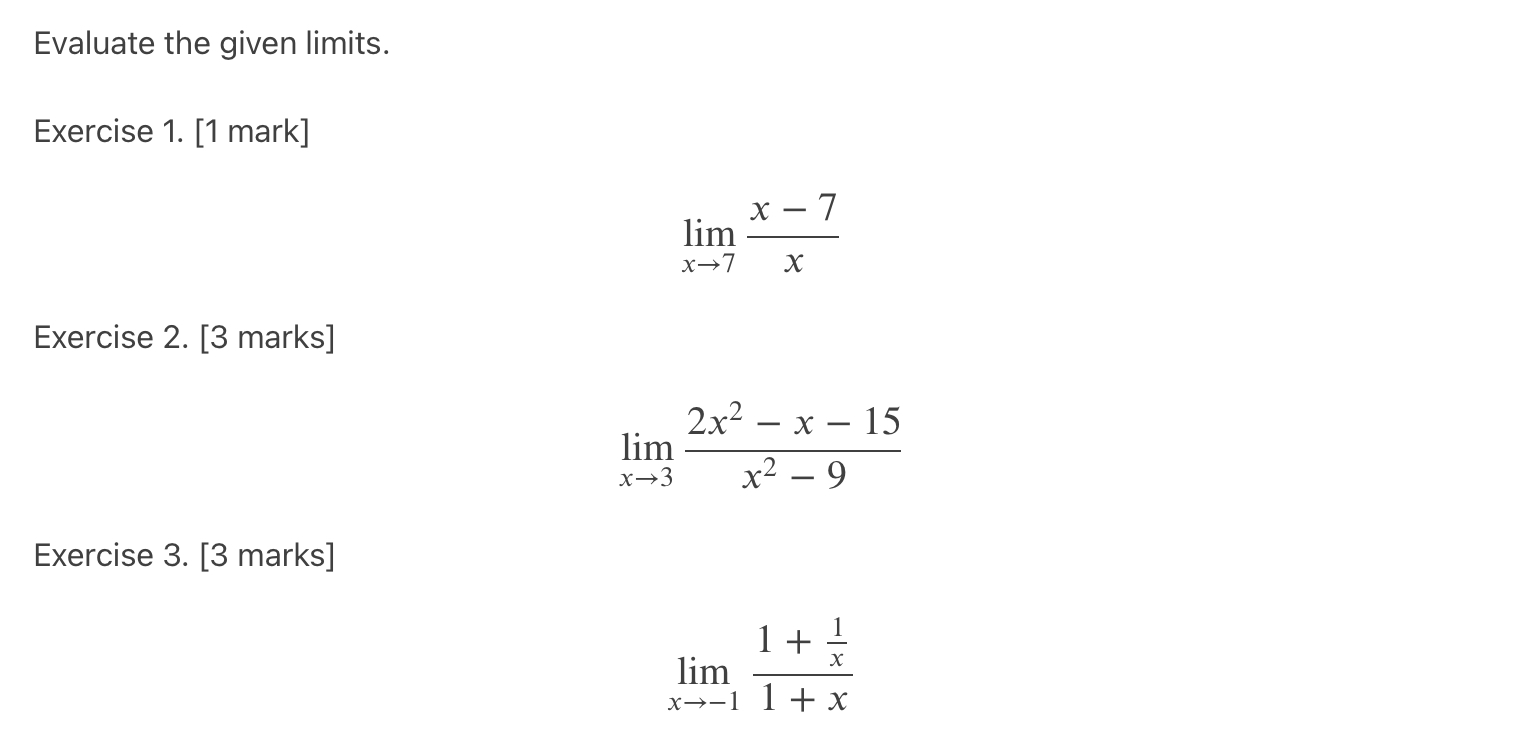
![mark] x - 7 lim x-7 X Exercise 2. [3 marks] 2x2](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666500d0030c8_375666500cfda993.jpg)

![marks] 1+ - lim x--1 1+x-8- -6 ( - 2, 4 )](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666500d0d35f9_376666500d0b140b.jpg)

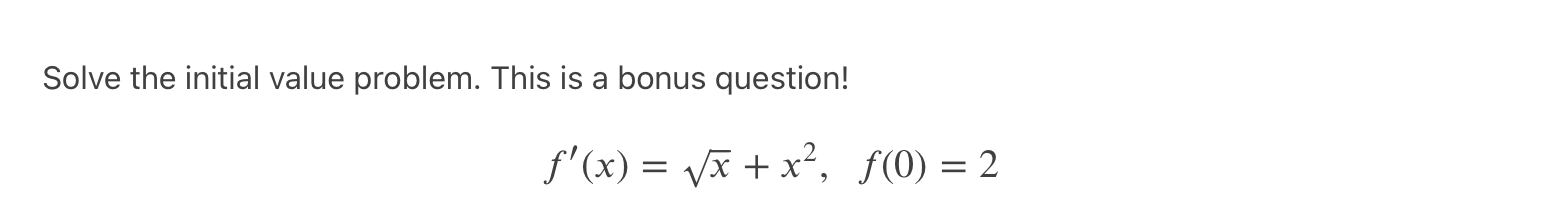
please show work/steps clearly
![the domain of the given piecewise function in interval notation. [2 marks].](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666500d1d13b2_377666500d1a74c2.jpg)
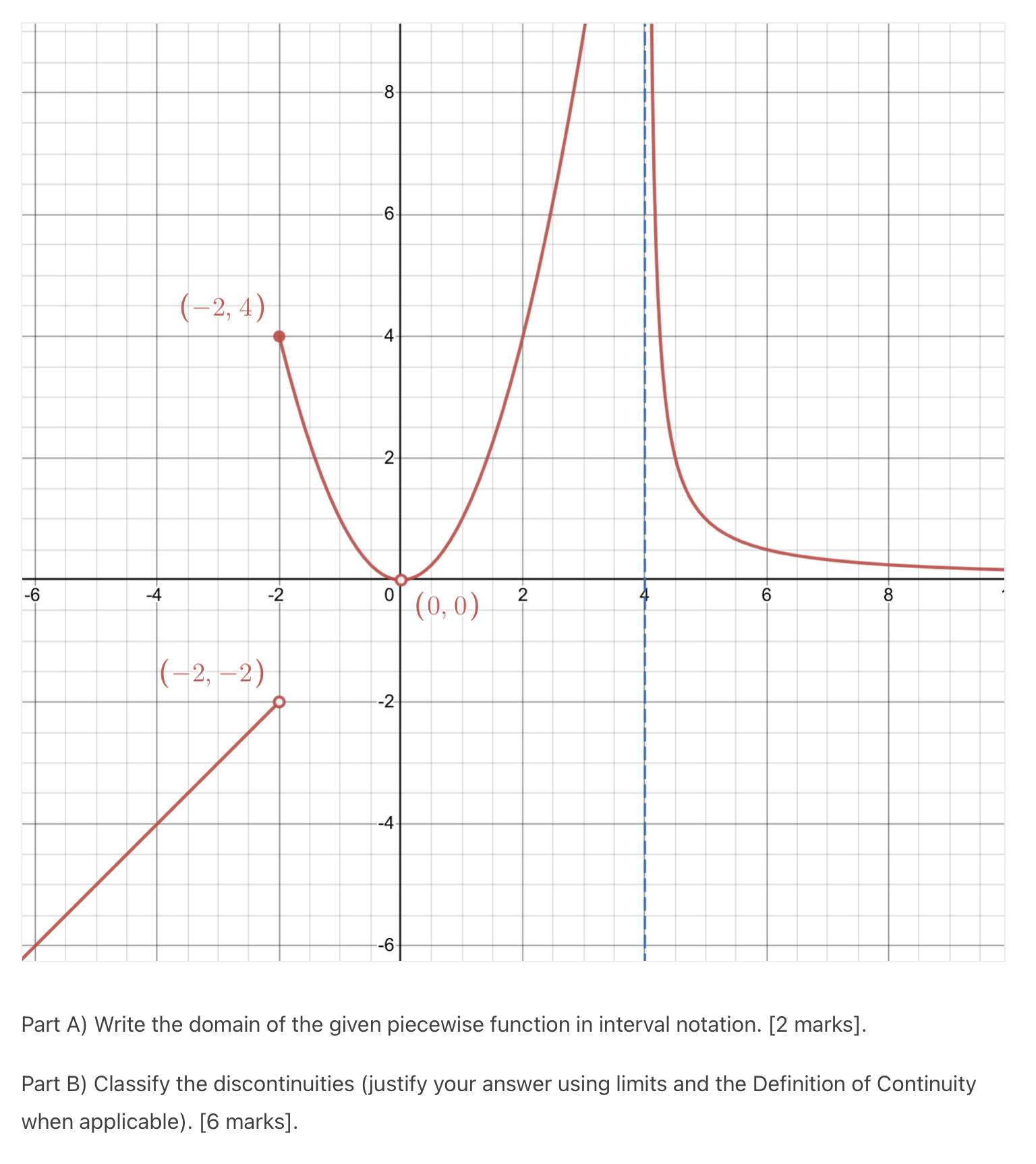
![Definition of Continuity when applicable). [6 marks].Calculate the derivative of the given](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666500d2bb05d_378666500d28adcc.jpg)

![derivative. . _ 2+2 ExerCIse 1. [2 marks]. f(x) x65): x Exercise](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666500d3827bd_379666500d36f7fa.jpg)
![2. [2 marks]. g(x) = V5 x2 + x + 1 -](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666500d3cedc4_379666500d3b1d76.jpg)
Evaluate the given limits. Exercise 1. [1 mark] x - 7 lim x-7 X Exercise 2. [3 marks] 2x2 - x - 15 lim x-+3 x2 - 9 Exercise 3. [3 marks] 1+ - lim x--1 1+x-8- -6 ( - 2, 4 ) -4 2 -6 -4 -2 0 (0, 0) 2 6 CO - ( - 2 , - 2) -2 -4. -6 Part A) Write the domain of the given piecewise function in interval notation. [2 marks]. Part B) Classify the discontinuities (justify your answer using limits and the Definition of Continuity when applicable). [6 marks].Calculate the derivative of the given functions. You do not need to simplify your answer after calculating the derivative. . _ 2+2 ExerCIse 1. [2 marks]. f(x) x65): x Exercise 2. [2 marks]. g(x) = V5 x2 + x + 1 - 1n(x 2) Exercise 3. [2 marks]. h(x) = Sin(COS(7rx)) Exercise 4. [3 marks]. Use implicit differentiation for this function: tan(y) = yxz. You have to isolate the derivative in your final answer. Exercise 5. [3 marks]. Use logarithmic differentiation for the function y = 36\"\" x. Write your final answer as a function of x. Sketch the graph of the rational function x2 x24 x} = by determining the answers to the following parts. You must show calculations for each step and your graph must be derived from your work (meaning, do not graph using Desmos). (A) State the domain in interval notation. [1 mark]. (B) Determine any intercepts, written as points [2 marks]. (C) State the equations of any vertical asymptotes and use one-sided limits to determine the local behavior around the asymptotes. [5 marks]. (D) Use limits at infinity to calculate the equation of any horizontal asymptotes. [2 marks]. (E) Use the first derivative and a sign chart to determine the intervals where the function increases and decreases. [6 marks]. (F) Using the results from your sign chart in (E), list any local extrema as points. [1 mark]. (G) Use the second derivative and a sign chart to determine the intervals where the function is concave up and down. [6 marks]. (H) List any inflection points. [1 mark]. (I) Graph the function. Make sure you label everything you found in the steps above. [3 marks]. For f(x) = sin(x) over the interval [0, 2], show that the Mean Value Theorem applies and use it to find the value of c guaranteed by the theorem.Solve the initial value problem. This is a bonus question! f' (x) = Vx+x, f(0) =2
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


