Please solve all of this using matlab and post the code since it requires a code. Thank you!! (Sorry for the long question by the way :( )

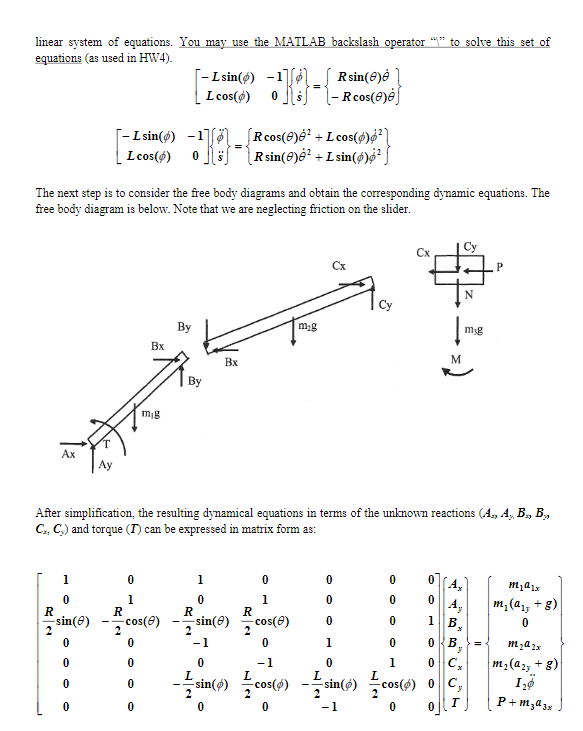
Consider the planar linkage shown below. The crank (link with length R) will tum counter-clockwise with a constant angular velocity (). The slider will experience a force (Pi of 110 N directed to the left. Your (a calculates the required input torque (T) and the magnitudes of the pin reaction forces (A, B, (b) You will then use your program to determine how changing the dimension H changes the task is to write a MATLAB program that and C, along both x and y directions) for two full revolutions (0 4) ofthe crank. average magnitudes of the pin reaction forces (refer to the free body diagram for the locations of these pins). Slider R-0.5m L-1.25mm H- 0.25m 0-2 rad/sec The first task is to determine the angled and the slider position given the crank angle. The constraint equations that must be satisfied are: R sin()+ L sin(0)-H R cos@)-L cos@) = s ou are Newton-Raphson method (as used in HW3) The next task is to solve for the (first and second) time derivatives of and 5. given (whose value is a constant, see in the figure on page1). Equations (1) and (2) may be differentiated to obtain the following Consider the planar linkage shown below. The crank (link with length R) will tum counter-clockwise with a constant angular velocity (). The slider will experience a force (Pi of 110 N directed to the left. Your (a calculates the required input torque (T) and the magnitudes of the pin reaction forces (A, B, (b) You will then use your program to determine how changing the dimension H changes the task is to write a MATLAB program that and C, along both x and y directions) for two full revolutions (0 4) ofthe crank. average magnitudes of the pin reaction forces (refer to the free body diagram for the locations of these pins). Slider R-0.5m L-1.25mm H- 0.25m 0-2 rad/sec The first task is to determine the angled and the slider position given the crank angle. The constraint equations that must be satisfied are: R sin()+ L sin(0)-H R cos@)-L cos@) = s ou are Newton-Raphson method (as used in HW3) The next task is to solve for the (first and second) time derivatives of and 5. given (whose value is a constant, see in the figure on page1). Equations (1) and (2) may be differentiated to obtain the following