Question: Please solve and answer Problem 3: Paper-Folding Patterns Take a piece of paper, and fold it in half as many times as you can. After

Please solve and answer
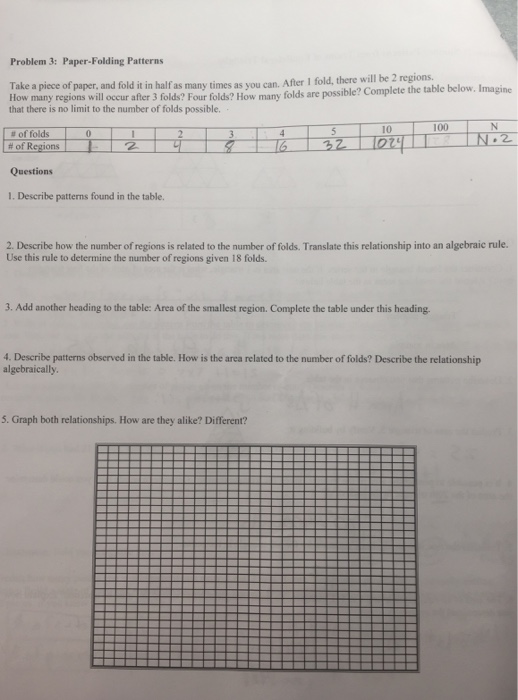
Problem 3: Paper-Folding Patterns Take a piece of paper, and fold it

Problem 3: Paper-Folding Patterns Take a piece of paper, and fold it in half as many times as you can. After I fold, there will be 2 regions. How many regions will occur after 3 folds? Four folds? How many folds are possible? Complete the table below. Imagine that there is no limit to the number of folds possible. # of folds 0 # of Regions 2 Questions 1. Describe patterns found in the table. 3. 4 5 10 100 N 16 32 1024 N.2 2. Describe how the number of regions is related to the number of folds. Translate this relationship into an algebraic rule. Use this rule to determine the number of regions given 18 folds. 3. Add another heading to the table: Area of the smallest region. Complete the table under this heading. 4. Describe patterns observed in the table. How is the area related to the number of folds? Describe the relationship algebraically. 5. Graph both relationships. How are they alike? Different?

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

A three-dimensional elasticity problem of a uniform bar stretched under its own weight gives the following strain field: where A and B are constants. Integrate the strainedisplacement relations to...

The City of Saltwater Beach established an enterprise fund in 2015 to construct and operate Tribute Aquatic Center, a public swimming pool. The pool was completed and began operations in 2016. All...

Franchising is often thought of as a retail activity, but B2B franchising is now flour- ishing. If it is a good idea, why has it spread more slowly than B2C franchising?

43. For P(Y A) > 0, show that E[X|Y A] = E[X I{Y A}] P(Y A) where I{B} is the indicator variable of the event B, equal to 1 if B occurs and to 0 otherwise.

Rich, a club member, left his golf clubs with Bogan, the pro at the Happy Hours Country Club, to be refinished at Bogans pro shop. The refinisher employed by Bogan suddenly left town, taking Richs...

Which of the following best defines organizational culture? basic beliefs about what is right or wrong within a business or corporation characteristic values, traditions, and behaviors a firm's...

Refer to the description of Century National Bank at the end of the Review of Chapters 14 on page 128. With many other options available, customers no longer let their money sit in a checking...

Garland Company Balance Sheet, Year Ended Dec 31, 2019 Assets: Cash and marketable securities $ 500,000 Accounts receivable 800,000 Inventories 1,350,000 Prepaid expenses 50,000 Total current assets...

A lab orders a number of chemicals from the same supplier, with a lead time two weeks. The assistant manager of the lab must determine how much of one of these chemicals to order. Usage of the...

Spec, Inc.s stock is expected to generate a dividend and terminal value one year from now of P57.00.The stock has a beta of 1.3, the risk-free interest rate is 6 percent, and the expected return...

1. Honda is planning to introduce new electric car in 2 years. Describe your role in detail as Procurement and Purchasing Manager of Honda to ensure this product will be ready to launch in two years....

The production records of Prince Company for the month of June shows the following: Total Manufacturing Cost Variance P 3,840 U Rate Variance 8,710 F Total material cost variance 2,975 U Total Labor...

Based on the facts, what is the primary ethical issue in this case? Who are the stakeholders? What changes could have been made to impact the outcome of this fraud? Research recent developments in...

Payback period Each of the following scenarios dependent. Assume that all cash flows are tak cashews Colby Hepworth at invested $600,000 in a book and store the best rece cash come of $120,000 per...

Open Text Corporation provides a suite of business information software products. Exhibit 10-9 contains Note 10 from the companys 2013 annual report detailing long-term debt. Required: a. Open Text...

5 The directors of Fama Industries plc are currently considering the acquisition of Beaver plc as part of its expansion programme. Fama Industries plc has interests in machine tools and light...

6 Europium plc is a large conglomerate which is seeking to acquire other companies. The Business Development division of Europium plc has recently identified an engineering company Promithium plc ...

4 Larkin Conglomerates plc owns a subsidiary company, Hughes Ltd, which sells office equipment. Recently, Larkin Conglomerates plc has been reconsidering its future strategy and has decided that...