please solve Floating-point addition (using Manos machine emulator) make sure it is correct

thanks

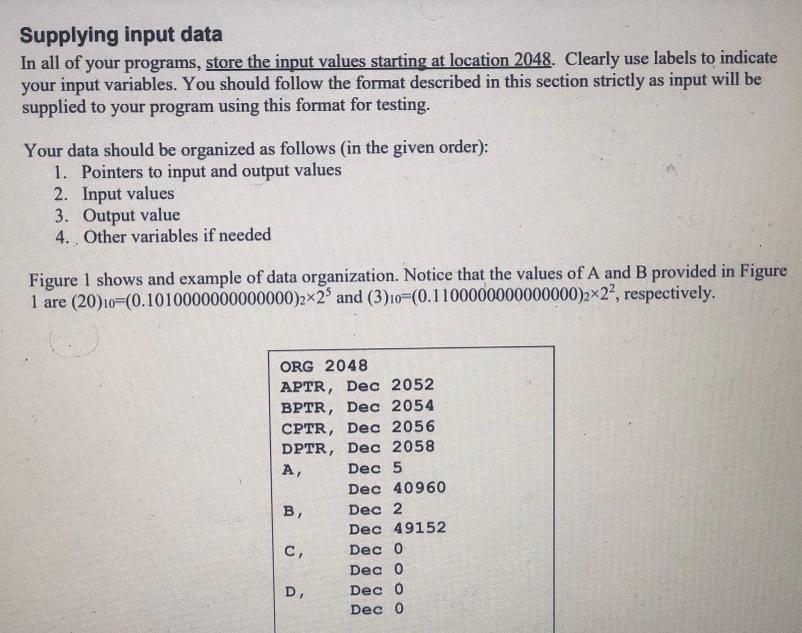
3 Project description Assume floating-point (non-standard) representation of numbers as follows: Each number is represented by two consecutive 16-bit words The first word represents the exponent (using 2's representation). The second word represents an unsigned mantissa The floating point numbers are represented using our special normalized form (0.1xxx...x), by which, o If the floating-point number is not zero, the most significant bit of the mantissa is 1 and the binary point is placed right before this leftmost bit. o If the floating-point number is zero, both the mantissa and the exponent fields should have a zero value. Notice that the above floating-point representation is not a standard one. Therefore, it may not be the most effective one (in terms of utilizing the available bits to achieve optimal accuracy and range of values). It is specifically designed to simplify your project implementation. Examples: The decimal number (13.25)10=(1101.01)2 is represented as follows: (1101.01)2=0.110101 x 24 (normalized) Therefore, the 16 bit exponent is 0000000000000100 (which is +4 in 2's complement). The 16 bit mantissa is 1101010000000000. The decimal number (0.312510=(0.0101)2 is represented as follows: (0.0101)2=0.101 x 2" (normalized) Therefore, the 16 bit exponent is 111111111 11111 (which is -1 in 2's complement). The 16 bit mantissa is 1010000000000000 The number zero is represented as Exponent=0000000000000000 Mantissa = 0000000000000000 . Write assembly language programs to perform each of the following floating-point operations on two input floating point numbers A and B: 1. Compute C=A+B and produce a normalized floating point result C 2. Compute D=AB and produce a normalized floating point result D (notice that in order to be able to perform this operation, you need to implement a subroutine that performs multiplication of two unsigned integers) You can make the following assumptions: 1. The mantissa's are unsigned (i.c., no negative values) 2. A and B are non-zero values and A is greater than B 3. The mantissa of input values A and B require no more than 8-bits (i.e., they are smaller than 256. Therefore, their multiplication will not result in a value that requires more than 16 bits. 4. No overflow or underflow could occur. Therefore, you can ignore checking for these. Add Algorithm 1. Align the binary point of the two values by shifting the mantissa of the smaller value (i.e. B) right by a number of positions equal to the difference between exponents. With this you can imagine that both values have the same exponents and, therefore, the locations of their binary points are aligned. Make sure that for the first position shift, you should shift in a l" value (the implicit most significant bit). 2. Compute the result a. The result mantissa of the result is the addition of both mantissa's b. The result exponent is the common exponent after aligning the binary point, which is the exponent of A. 3. Normalize the result by shifting the result right by one position (if needed) and adjusting (incrementing) the exponent. Notice that considering the above assumptions, you only need to do shift the result by a maximum of one position if there is a carry when you add the mantissa's. Supplying input data In all of your programs, store the input values starting at location 2048. Clearly use labels to indicate your input variables. You should follow the format described in this section strictly as input will be supplied to your program using this format for testing. Your data should be organized as follows (in the given order): 1. Pointers to input and output values 2. Input values 3. Output value 4. Other variables if needed Figure 1 shows and example of data organization. Notice that the values of A and B provided in Figure 1 are (20)10=(0.1010000000000000)2x2 and (3)10=(0.1100000000000000)2x22, respectively. ORG 2048 APTR, Dec 2052 BPTR, Dec 2054 CPTR, Dec 2056 DPTR, Dec 2058 A, Dec 5 Dec 40960 B Dec 2 Dec 49152 Dec 0 Dec 0 D Dec 0 Dec 0 c, D 3 Project description Assume floating-point (non-standard) representation of numbers as follows: Each number is represented by two consecutive 16-bit words The first word represents the exponent (using 2's representation). The second word represents an unsigned mantissa The floating point numbers are represented using our special normalized form (0.1xxx...x), by which, o If the floating-point number is not zero, the most significant bit of the mantissa is 1 and the binary point is placed right before this leftmost bit. o If the floating-point number is zero, both the mantissa and the exponent fields should have a zero value. Notice that the above floating-point representation is not a standard one. Therefore, it may not be the most effective one (in terms of utilizing the available bits to achieve optimal accuracy and range of values). It is specifically designed to simplify your project implementation. Examples: The decimal number (13.25)10=(1101.01)2 is represented as follows: (1101.01)2=0.110101 x 24 (normalized) Therefore, the 16 bit exponent is 0000000000000100 (which is +4 in 2's complement). The 16 bit mantissa is 1101010000000000. The decimal number (0.312510=(0.0101)2 is represented as follows: (0.0101)2=0.101 x 2" (normalized) Therefore, the 16 bit exponent is 111111111 11111 (which is -1 in 2's complement). The 16 bit mantissa is 1010000000000000 The number zero is represented as Exponent=0000000000000000 Mantissa = 0000000000000000 . Write assembly language programs to perform each of the following floating-point operations on two input floating point numbers A and B: 1. Compute C=A+B and produce a normalized floating point result C 2. Compute D=AB and produce a normalized floating point result D (notice that in order to be able to perform this operation, you need to implement a subroutine that performs multiplication of two unsigned integers) You can make the following assumptions: 1. The mantissa's are unsigned (i.c., no negative values) 2. A and B are non-zero values and A is greater than B 3. The mantissa of input values A and B require no more than 8-bits (i.e., they are smaller than 256. Therefore, their multiplication will not result in a value that requires more than 16 bits. 4. No overflow or underflow could occur. Therefore, you can ignore checking for these. Add Algorithm 1. Align the binary point of the two values by shifting the mantissa of the smaller value (i.e. B) right by a number of positions equal to the difference between exponents. With this you can imagine that both values have the same exponents and, therefore, the locations of their binary points are aligned. Make sure that for the first position shift, you should shift in a l" value (the implicit most significant bit). 2. Compute the result a. The result mantissa of the result is the addition of both mantissa's b. The result exponent is the common exponent after aligning the binary point, which is the exponent of A. 3. Normalize the result by shifting the result right by one position (if needed) and adjusting (incrementing) the exponent. Notice that considering the above assumptions, you only need to do shift the result by a maximum of one position if there is a carry when you add the mantissa's. Supplying input data In all of your programs, store the input values starting at location 2048. Clearly use labels to indicate your input variables. You should follow the format described in this section strictly as input will be supplied to your program using this format for testing. Your data should be organized as follows (in the given order): 1. Pointers to input and output values 2. Input values 3. Output value 4. Other variables if needed Figure 1 shows and example of data organization. Notice that the values of A and B provided in Figure 1 are (20)10=(0.1010000000000000)2x2 and (3)10=(0.1100000000000000)2x22, respectively. ORG 2048 APTR, Dec 2052 BPTR, Dec 2054 CPTR, Dec 2056 DPTR, Dec 2058 A, Dec 5 Dec 40960 B Dec 2 Dec 49152 Dec 0 Dec 0 D Dec 0 Dec 0 c, D