Please solve it through mathlab symbolic algebra

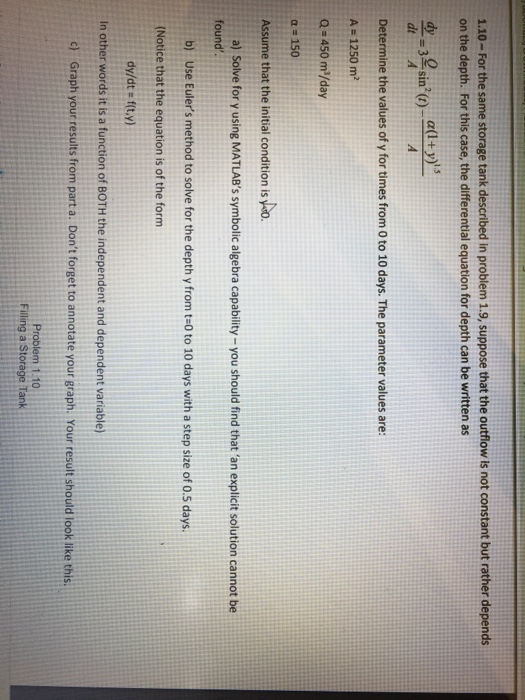
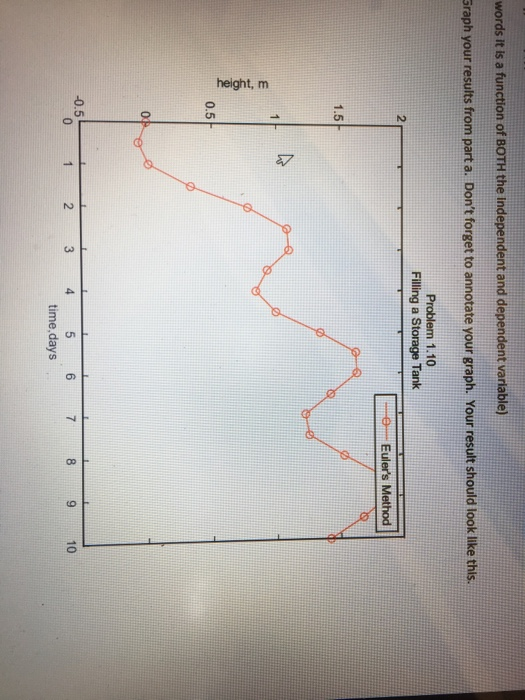
1.10-For the same storage tank described in problem 1.9, suppose that the outflow is not constant but rather depends on the depth. For this case, the differential equation for depth can be written as -3 sin (t)- dtA Determine the values of y for times from 0 to 10 days. The parameter values are: A 1250 m2 Q- 450 m2/day 150 Assume that the initial condition is o. a) Solve for y using MATLAB's symbolic algebra capability-you should find that 'an explicit solution cannot be found. b) Use Euler's method to solve for the depth y from t-0 to 10 days with a step size of 0.5 days. (Notice that the equation is of the form dy/dt fit,y) In other words it is a function of BOTH the independent and dependent variable c) Graph your results from part a. Don't forget to annotate your graph. Your result should look like this. words it is a function of BOTH the independent and dependent variable) raph your results from part a. Don't forget to annotate your graph. Your result should look like this Problem 1.10 Filling a S Tank 2 1.5 0.5 0 0.5 0 2 8 9 10 time,days 1.10-For the same storage tank described in problem 1.9, suppose that the outflow is not constant but rather depends on the depth. For this case, the differential equation for depth can be written as -3 sin (t)- dtA Determine the values of y for times from 0 to 10 days. The parameter values are: A 1250 m2 Q- 450 m2/day 150 Assume that the initial condition is o. a) Solve for y using MATLAB's symbolic algebra capability-you should find that 'an explicit solution cannot be found. b) Use Euler's method to solve for the depth y from t-0 to 10 days with a step size of 0.5 days. (Notice that the equation is of the form dy/dt fit,y) In other words it is a function of BOTH the independent and dependent variable c) Graph your results from part a. Don't forget to annotate your graph. Your result should look like this. words it is a function of BOTH the independent and dependent variable) raph your results from part a. Don't forget to annotate your graph. Your result should look like this Problem 1.10 Filling a S Tank 2 1.5 0.5 0 0.5 0 2 8 9 10 time,days