PLEASE SOLVE IT WITH SENSITIVITY ANALYSIS. TYSM!

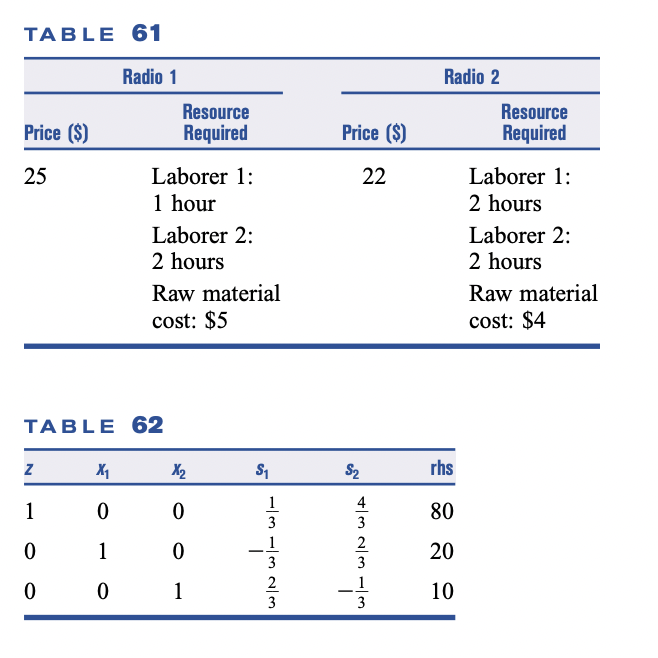
22 Radioco manufactures two types of radios. The only scarce resource that is needed to produce radios is labor. The company now has two laborers. Laborer 1 is willing to work up to 40 hours per week and is paid $5 per hour. Laborer 2 is willing to work up to 50 hours per week and is paid $6 per hour. The price as well as the resources required to build each type of radio are given in Table 61. a Letting xi be the number of type i radios produced each week, show that Radioco should solve the following LP (its optimal tableau is given in Table 62): maxz=3x1+2x2s.t.x1+2x2402x1+x250x1,x20 b For what values of the price of a Type 1 radio would the current basis remain optimal? c For what values of the price of a Type 2 radio would the current basis remain optimal? d If laborer 1 were willing to work only 30 hours per week, would the current basis remain optimal? e If laborer 2 were willing to work as many as 60 hours per week, would the current basis remain optimal? f If laborer 1 were willing to work an additional hour, what is the most that Radioco should pay? g If laborer 2 were willing to work only 48 hours, what would Radioco's profits be? Verify your answer by determining the number of radios of each type that would be produced. h A Type 3 radio is under consideration for production. The specifications of a Type 3 radio are as follows: price, $30;2 hours from laborer 1;2 hours from laborer 2 ; cost of raw materials, $3. Should Radioco manufacture any Type 3 radios? TAB LE 61 TABLE 62 \begin{tabular}{rrrrrr} \hlinez & x1 & x2 & \multicolumn{1}{c}{s1} & s2 & rhs \\ \hline 1 & 0 & 0 & 31 & 34 & 80 \\ 0 & 1 & 0 & 31 & 32 & 20 \\ 0 & 0 & 1 & 32 & 31 & 10 \\ \hline \end{tabular} 22 Radioco manufactures two types of radios. The only scarce resource that is needed to produce radios is labor. The company now has two laborers. Laborer 1 is willing to work up to 40 hours per week and is paid $5 per hour. Laborer 2 is willing to work up to 50 hours per week and is paid $6 per hour. The price as well as the resources required to build each type of radio are given in Table 61. a Letting xi be the number of type i radios produced each week, show that Radioco should solve the following LP (its optimal tableau is given in Table 62): maxz=3x1+2x2s.t.x1+2x2402x1+x250x1,x20 b For what values of the price of a Type 1 radio would the current basis remain optimal? c For what values of the price of a Type 2 radio would the current basis remain optimal? d If laborer 1 were willing to work only 30 hours per week, would the current basis remain optimal? e If laborer 2 were willing to work as many as 60 hours per week, would the current basis remain optimal? f If laborer 1 were willing to work an additional hour, what is the most that Radioco should pay? g If laborer 2 were willing to work only 48 hours, what would Radioco's profits be? Verify your answer by determining the number of radios of each type that would be produced. h A Type 3 radio is under consideration for production. The specifications of a Type 3 radio are as follows: price, $30;2 hours from laborer 1;2 hours from laborer 2 ; cost of raw materials, $3. Should Radioco manufacture any Type 3 radios? TAB LE 61 TABLE 62 \begin{tabular}{rrrrrr} \hlinez & x1 & x2 & \multicolumn{1}{c}{s1} & s2 & rhs \\ \hline 1 & 0 & 0 & 31 & 34 & 80 \\ 0 & 1 & 0 & 31 & 32 & 20 \\ 0 & 0 & 1 & 32 & 31 & 10 \\ \hline \end{tabular}