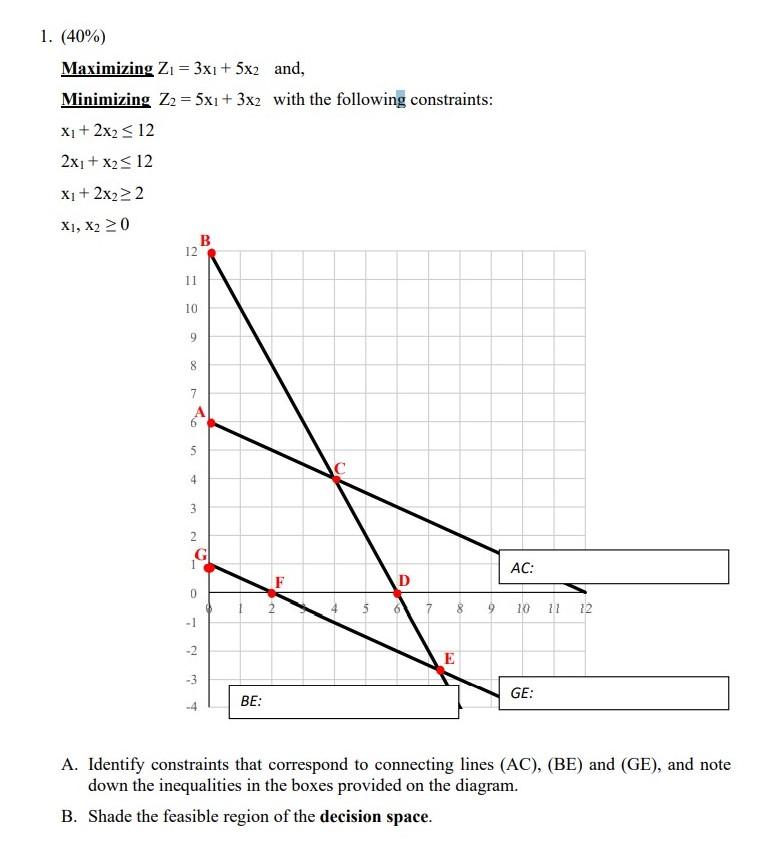
Question: Please solve part a, b, c and d 1. (40%) Maximizing Z1 = 3x1 + 5x2 and, Minimizing Z2 = 5x1 + 3x2 with the

Please solve part a, b, c and d
1. (40%) Maximizing Z1 = 3x1 + 5x2 and, Minimizing Z2 = 5x1 + 3x2 with the following constraints: X1 + 2x2 2 X1, X2 > 0 B 12 1 10 9 8 7 64 si 4 3 2 G AC: D 0 ma 11 12 - 1 -2 E 2 -3 BE: GE: A. Identify constraints that correspond to connecting lines (AC), (BE) and (GE), and note down the inequalities in the boxes provided on the diagram. B. Shade the feasible region of the decision space. C. Note down the coordinates and the corresponding values of Z, and Z2 in a table: X2 Zi Z2 Non-inferior / Inferior / non-solution A B C D E F G D. Indicate in the table which solutions are non-inferior / inferior (and are dominated by which other solutions) / non-solution. E. Plot the corresponding feasible region in the objective space of Z, and Z2 on the enclosed graphing paper (do you need to normalize, in this particular question, why or why not?). F. By inspection only (graphically), thicken / highlight some of the connecting lines on the graph in part E to indicate the Pareto front (set of non-inferior solutions) corresponding to the two objective functions (one maximization and one minimization). G. Compare the results obtained from parts D and F, do they agree with each other is there any point indicated as non-inferior in part D but is inferior in part F)? Which result sounds more reasonable? Please briefly explain your rationale (please demonstrate your reasoning on the graph)Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


