Please solve Problem $4$ only. I also attached the prompts for Problems $2$ and $3$ for context.

Problem $4(25$ points, CCOs #$1$ & #$8)$

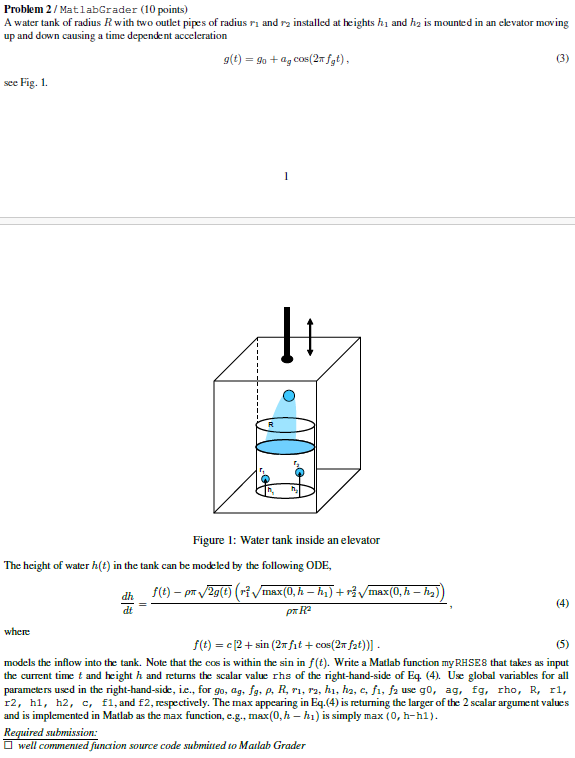
For the case described in problems $2$ and $3,$ calculate the height of water in the tank at t $=2500$s to within $10^(-7)$ m using either the third$-$order Runge$-$Kutta method of Problem $1,$ or$,$ for a $10$ point deduction, the classical RK$-4$ method. Outside of your code, report the method you have chosen to solve this problem, the final step size $\backslash$delta t employed and all supporting evidence that your result has the required accuracy. Note that for full credit it is not sufficient to only show that the estimated error is below the requested threshold, but you must also show that your chosen method converges as expected. Report h$($t $=2500$s$)$ as a floating point number in engineering notation with at least $10$ mantissa digits.

Here are the functions to use:

function $[$x$,$y$,$k$1,$k$2,$k$3,$slope$]=$ myRK$3($f$,$xi$,$yi$,$h$)$

$\%$ Perform a single step of the $3$rd$-$order Runge$-$Kutta method

$\%$ Inputs:

$\%$ f $=$ Function handle representing d$($y$)/($d$)$x $=$ f$($x$,$y$)$

$\%$ xi $=$ Current independent variable value $($x$\_($i$))$

$\%$ yi $=$ Current dependent variable value $($y$\_($i$))$

$\%$ h $=$ Step size

$\%$ Outputs:

$\%$ x $=$ Updated independent variable value $($x$\_($i$+1))$

$\%$ y $=$ Updated dependent variable value $($y$\_($i$+1))$

$\%$ Coefficients from the Butcher tableau

a$1=0$;

a$2=(1)/(2)$;

a$3=(3)/(4)$;

b$21=(1)/(2)$;

b$31=0$;

b$32=(3)/(4)$;

c$1=(2)/(9)$;

c$2=(1)/(3)$;

c$3=(4)/(9)$;

$\%$ Compute k$1,$ k$2,$ k$3$

k$1=$ f$($xi$,$yi$)$;

k$2=$ f$($xi $+$ a$2*$ h$,$ yi $+$ b$21*$ h $*$ k$1)$;

k$3=$ f$($xi $+$ a$3*$ h$,$ yi $+$ b$31*$ h $*$ k$1+$ b$32*$ h $*$ k$2)$;

$\%$ Compute the slope using the weights

slope $=$ c$1*$ k$1+$ c$2*$ k$2+$ c$3*$ k$3$;

$\%$ Update x and y values

x $=$ xi $+$ h;

y $=$ yi $+$ h $*$ slope;

end

function rhs $=$ myRHSE$8($t$,$h$)$

$\%$ Calculate the right$-$hand$-$side of the ODE for water height in the tank

$\%$ Inputs:

$\%$ t $=$ Current time $($scalar$)$

$\%$ h $=$ Current water height in the tank $($scalar$)$

$\%$ Output:

$\%$ rhs $=$ The right$-$hand$-$side of the ODE, representing d$($h$)/($d$)$t $($scalar$)$

$\%$ Declare global variables

global g$0$ ag fg rho R r$1$ r$2$ h$1$ h$2$ c f$1$ f$2$;

$\%$ Calculate time$-$dependent acceleration g$($t$)$

g$\_($t$)=$ g$0+$ ag $*$ cos$(2*$ pi $*$ fg $*$ t$)$;

$\%$ Calculate the inflow rate f$($t$)$

f$\_($t$)=$ c $*(2+$ sin$(2*$ pi $*$ f$1*$ t $+$ cos$(2*$ pi $*$ f$2*$ t$)))$;

$\%$ Calculate the outflow terms for visual simplicity

outflow$1=$ r$1^(2)*$ sqrt$($max$(0,$h $-$ h$1))$;

outflow$2=$ r$2^(2)*$ sqrt$($max$(0,$h $-$ h$2))$;

$\%$ Compute the RHS of the ODE

rhs $=($f$\_($t$)-($rho $*$ pi $*$ sqrt$(2*$ g$\_($t$)))*($outflow$1+$ outflow$2))()/()($rho $*$ pi $*$ R$^(2))$;

end

This is the script I used to solve Problem $3$:

$\%$ Declare global variables

global g$0$ ag fg rho R r$1$ r$2$ h$1$ h$2$ c f$1$ f$2$;

$\%$ Define the given parameters

g$0=9\mathrm{.}81$; $\%($ m$)/($s$^(2))$

ag $=4$; $\%($ m$)/($s$^(2))$

fg $=0\mathrm{.}0017$; $\%$ Hz

rho $=1000$; $\%$ k$($g$)/($m$^(3))$

R $=1\mathrm{.}8$; $\%$ m

r$1=0\mathrm{.}09$; $\%$ m

r$2=0\mathrm{.}04$; $\%$ m

h$1=0\mathrm{.}13$; $\%$ m

h$2=0\mathrm{.}2$; $\%$ m

c $=31$; $\%$ k$($g$)/($s$)$

f$1=0\mathrm{.}013$; $\%$ Hz

f$2=0\mathrm{.}024$; $\%$ Hz

$\%$ Initial conditions and simulation parameters

t$0=0$; $\%$ Initial time $($s$)$

h$0=0\mathrm{.}35$; $\%$ Initial height of water in the tank $($m$)$

t$\_($f$)$inal $=2500$; $\%$ Final time $($s$)$

dt $=10$; $\%$ Step size $($s$)$

$\%$ Function handle for the ODE

f $=$ @$($t$,$h$)$ myRHSE$8($t$,$h$)$;

$\%$ Initialize variables

t $=$ t$0$; $\%$ Start time

h $=$ h$0$; $\%$ Start height

$\%$ Time$-$stepping loop using $3$rd$-$order Runge$-$Kutta

while t $$ t$\_($f$)$inal

$[$t$\_($n$)$ext$,$h$\_($n$)$ext$]=$ myRK$3($f$,$t$,$h$,$dt$)$; $\%$ RK$3$ step

t $=$ t$\_($n$)$ext; $\%$ Update time

h $=$ h$\_($n$)$ext; $\%$ Update height

end

$\%$ Store the result in the variable 'answer'

answer $=$ h