Question: Please solve the following using proof of induction and explain each step for my understanding. Thanks! Question 1 (Complete Graphs) Question 2 (Graph Traversal) ---------------------------------------------------------------------------------------------------------------------------------------------

Please solve the following using proof of induction and explain each step for my understanding. Thanks!

Question 1 (Complete Graphs)

Please solve the following using proof of induction and explain each step

Question 2 (Graph Traversal) ---------------------------------------------------------------------------------------------------------------------------------------------

for my understanding. Thanks! Question 1 (Complete Graphs) Question 2 (Graph Traversal)

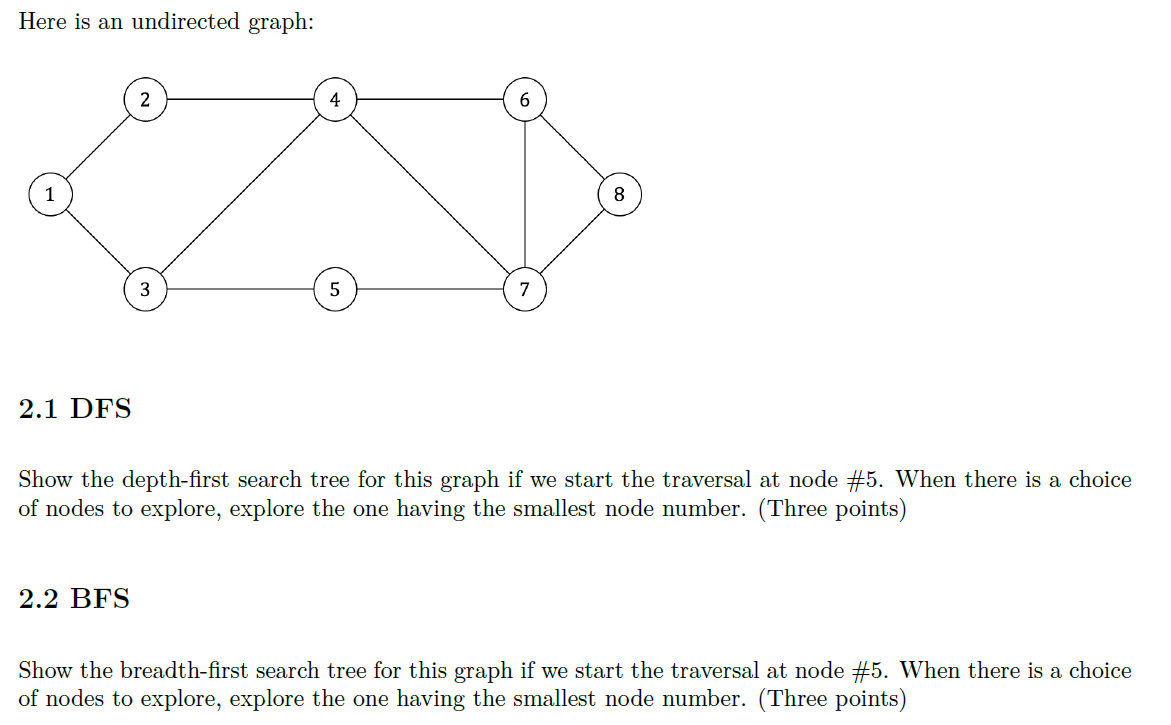
A graph G=(V,E) is complete if for all s,tV, there is an edge (s,t)E. Answer these questions: (1) How many edges does a complete graph G having n nodes have? Prove this inductively. State your inductive hypothesis clearly. (Five points) (2) How many iterations of DFS does it take to traverse a complete graph having n nodes? Explain (but don't prove) why this is. (One point) (3) How many iterations of BFS does it take to traverse a complete graph having n nodes? Explain (but don't prove) why this is. (One point) Here is an undirected graph: 2.1 DFS Show the depth-first search tree for this graph if we start the traversal at node \#5. When there is a choice of nodes to explore, explore the one having the smallest node number. (Three points) 2.2 BFS Show the breadth-first search tree for this graph if we start the traversal at node \#5. When there is a choice of nodes to explore, explore the one having the smallest node number. (Three points)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Please solve the following using proof of induction. Please also complete the bonus section at the bottom and explain each step for my understanding. Don't copy and paste any previous or similar...

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

Provide an appropriate query to show that the above program can give an incorrect result. [4 marks] (b) Explain the cause of the error. [6 marks] (c) Suggest a correction. [5 marks] (d) Write a...

You have been provided with the description of a programming language, J, intended for scripting applications. Its syntax is similar to a cut-down version of Java in that it consists of function...

ANSI-SPARC6 Programming Language Compilation Write notes on each of the following topics: (a) the implementation of labels and jumps in a recursive, block structured programming language [7 marks]...

1456HHSC attend all (a) In the quantum teleportation protocol, Alice and Bob are every in possession of one qubit of a couple in the joint country00i + statei. Explain how the protocol works. In...

Give the typing rules for Peano natural numbers and their eliminator.(ii) Using the rules given above, define the addition function.] (iii) Let a binary tree be either a leaf Leaf or a node...

Why is there a depletion layer in the immediate vicinity of the junction? 1 [TURN OVER CST.93.1.2 SECTION B 5 Give an ML definition of the function map3 which has the property that map3 f [x1, x2, ....

The next 4 questions, refer to the following problem: in the College of Winterhold, young apprentices, gifted in the magic arts, must follow a rigorous program before completing their degree on...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

Kay Wing, Inc., prepared the following balance sheet at December 31, 2013. Cash ............... $ 65,000 Accounts receivable ........... 37,000 Inventory .............. 70,000 Long-term investments...

A company desires to become more socially responsible. What particular things might it do to achieve this objective, and what benefits might be expected to result from these actions?

Which of the following events or bond contract features would increase the YTM on a corporate bond: Question 6 options: A provision in the bond that allows the bondholder to convert the bond into a...

On January 1, 2020, Harrison, Inc., acquired 90 percent of Starr Company in exchange for $1,125,000 fair-value consideration. The total fair value of Starr Company was assessed at $1,200,000....

2. I reject the harm that can result from reacting emotionally when I am upset and getting angry or feeling battered.

7. I understand that victims of my outbursts will remember my accusatory statements and name-calling long after I have calmed down.

6. I resist the temptation to feel entitled to better treatment and to lose emotional control.