Please, solve the question

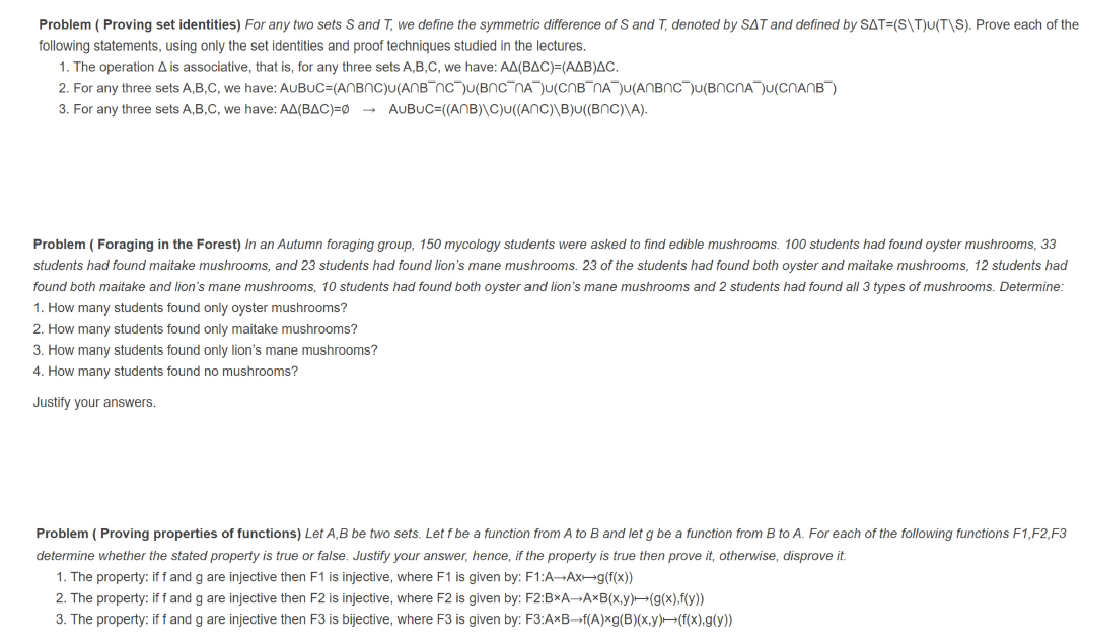
Problem ( Proving set identities) For any two sets S and T, we define the symmetric difference of S and T, denoted by SAT and defined by SAT=(S\\ T)(T\\S). Prove each of the following statements, using only the set identities and proof techniques studied in the lectures. 1. The operation A is associative, that is, for any three sets A,B,C, we have: AA(BAC)=(AAB)AC. 2. For any three sets A,B,C, we have: AUBUC=(AnBnC)(AnBEnC )U(BNC nA")(CABInA")(AnBNC )(BnCNA )(CnAnB ) 3. For any three sets A,B,C, we have: AA(BAC)=0 - AUBUC=((AnB)\\C)((AnC)\\Bju((BNC)\\A). Problem ( Foraging in the Forest) In an Autumn foraging group, 150 mycology students were asked to find edible mushrooms. 100 students had found oyster mushrooms, 33 students had found maitake mushrooms, and 23 students had found lion's mane mushrooms. 23 of the students had found both oyster and maitake mushrooms, 12 students had found both maitake and lion's mane mushrooms, 10 students had found both oyster and lion's mane mushrooms and 2 students had found all 3 types of mushrooms. Determine: 1. How many students found only oyster mushrooms? 2. How many students found only maitake mushrooms? 3. How many students found only lion's mane mushrooms? 4. How many students found no mushrooms? Justify your answers. Problem ( Proving properties of functions) Let A, B be two sets. Let f be a function from A to B and let g be a function from B to A. For each of the following functions F1,F2,F3 determine whether the stated property is true or false. Justify your answer, hence, if the property is true then prove it, otherwise, disprove it. 1. The property: if f and g are injective then F1 is injective, where F1 is given by: F1:A-Ax-g(f(x)) 2. The property: if f and g are injective then F2 is injective, where F2 is given by: F2:B*A-AxB(x,y)-(g(x),f(y)) 3. The property: if f and g are injective then F3 is bijective, where F3 is given by: F3:A*B-f(A)*g(B)(x.y)-(f(x).g(y))