PLEASE SOLVE THE QUESTION WITH JAVA! I DON'T WANT THE SOLUTION WITH C OR C++, I WANT JAVA! JAVA JAVA JAVA

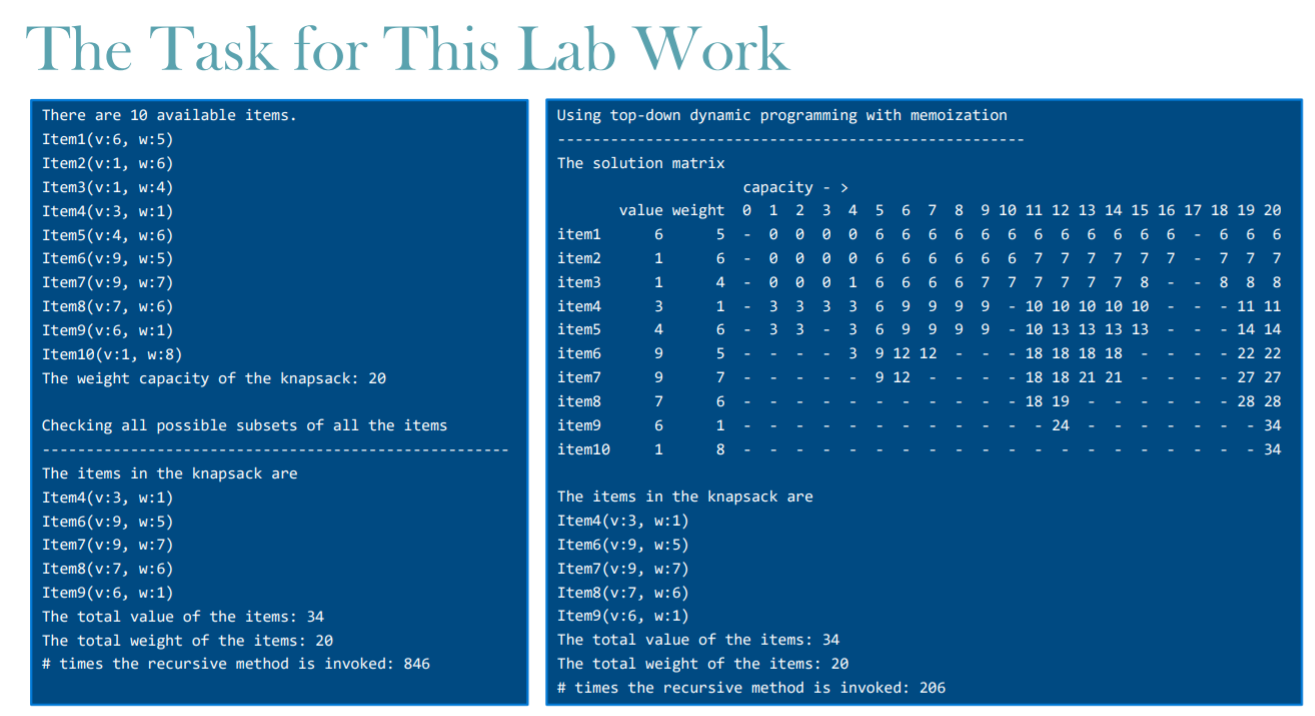
. . o Examine the given Lab12Template class (Lab12Template.java). Your task is to modify the two methods given with the following headers in this class: o private static int knapsackMemoization (int n, int capacity) o private static void printSolution(boolean printSolution Matrix) Write the body of the given knapsackMemoization method such that o it implements top-down dynamic programming with memoization as explained in the slides 12 and 13. o and it counts the number of the times the method is invoked recursively by using count2. The given printSolution method prints the solution of the 0-1 knapsack problem as shown in the slide 33. Modify this method such that it can deal with the empty values in the solution matrix as in the given example console output in the next slide. Note: When top-down dynamic programming with memoization is used, some values in the solution matrix remain with their default values (here the default value is null as the matrix has the type Integer) as the solution for the corresponding subproblems are not computed. This is due to the fact that some subproblems do not exist in practice and we are using a top-down approach not a bottom-up approach. The Task for This Lab Work Using top-down dynamic programming with memoization There are 10 available items. Item1(v:6, w:5) Item2(v:1, w:6) Item3(v:1, w:4) Item4(v:3, w:1) Item5(v:4, w:6) Item6(v:9, w:5) Item7(v:9, w:7) Item8(v:7, w:6) Item(v:6, w:1) Item10(v:1, w:8) The weight capacity of the knapsack: 20 - The solution matrix capacity - > value weight 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 item1 6 5 Looo 0 6 6 6 6 6 6 6 6 6 6 6 6 - 6 6 6 item2 1 6 . 0 0 0 6 6 6 6 6 6 7 7 7 7 7 7 . 7 7 7 item3 1 4 - 0 0 0 1 6 6 6 6 7 7 7 7 7 7 8 8 8 8 item4 3 1 - 3 3 3 3 6 9 9 9 9 - 10 10 10 10 10 - 11 11 item5 4 6 3 3 - 3 6 9 9 9 9 - 10 13 13 13 13 14 14 item6 9 5 3 9 12 12 - 18 18 18 18 22 22 item7 9 7 9 12 18 18 21 21 27 27 item8 7 6 18 19 28 28 item9 6 1 - 24 - 34 item10 1 8 34 Checking all possible subsets of all the items The items in the knapsack are Item4(v:3, w:1) Item(v:9, w:5) Item(v:9, w:7) Item8(v:7, w:6) Item(v:6, w:1) The total value of the items: 34 The total weight of the items: 20 # times the recursive method is invoked: 846 The items in the knapsack are Item4(v:3, w:1) Item6(v:9, w:5) Item(v:9, w:7) Items (v:7, w:6) Item(v:6, w:1) The total value of the items : 34 The total weight of the items: 20 # times the recursive method is invoked: 206