Please solve these and include an explanation

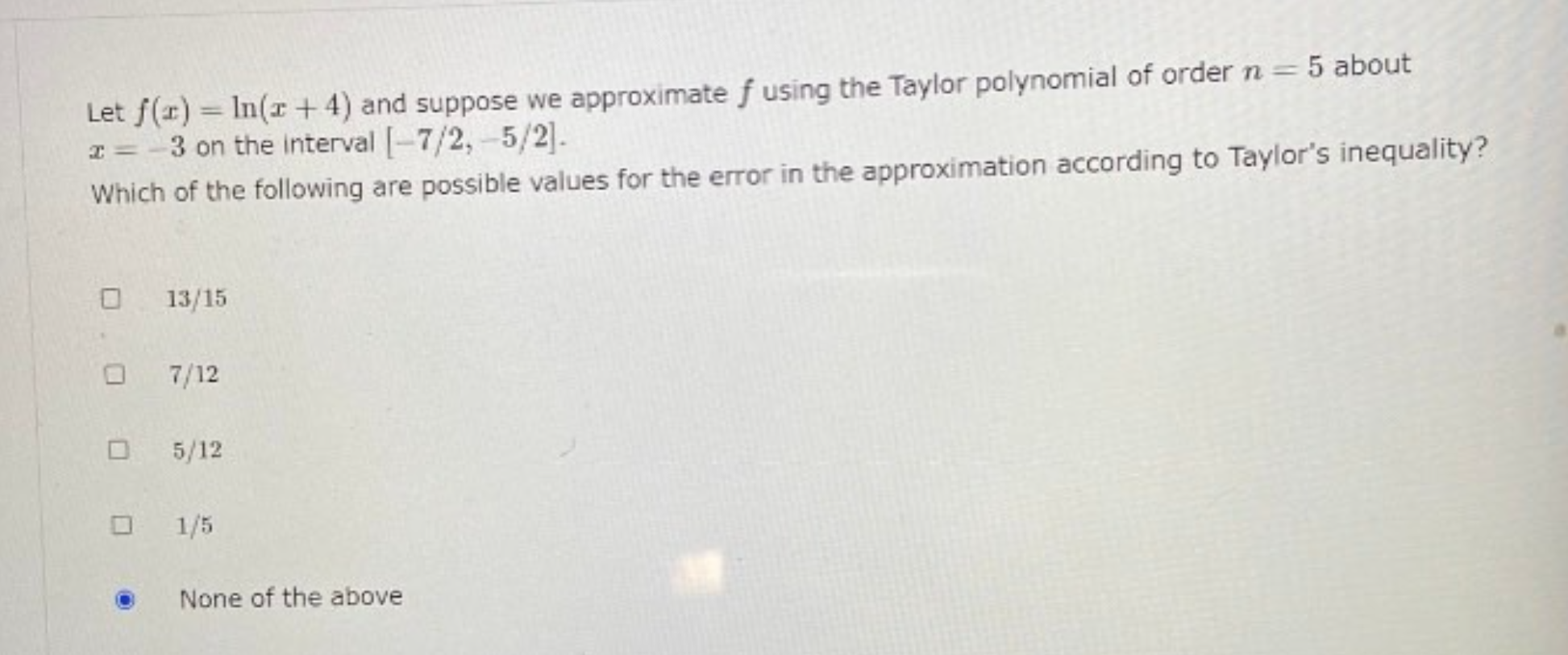
Let h(t) be the height of water at time t in a container that is being filled by water from the top at a constant rate. This question is concerned with properties of the graph of h(t) when the container has different shapes. Which of the following statements are true? If the container is cylindrical, h is neither ( concave upward nor concave downward for all t. O If the container is a sphere, h has a point of inflection. If the container is a cone with the tip down, O h is concave downward for all t. If the container is a sphere, h is initially O concave downward. None of the aboveLet f(er) = In(x + 4) and suppose we approximate f using the Taylor polynomial of order n = 5 about z = -3 on the interval [-7/2, 5/2]. Which of the following are possible values for the error in the approximation according to Taylor's inequality? 0 13/15 0 7/12 0 5/12 0 1/5 None of the above