please solve this ptoblem ***MANUALLY***

and there is table related to the question

course :Optmization Mathod

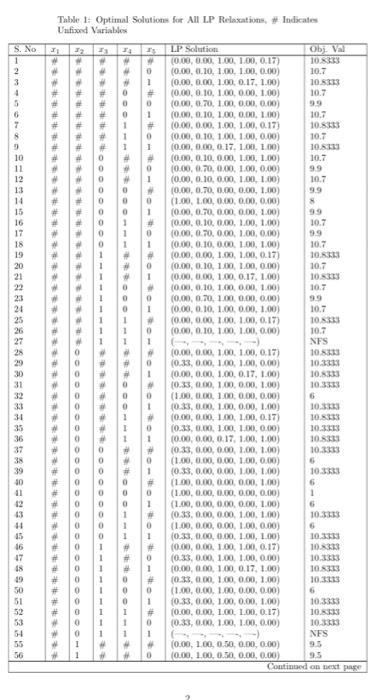
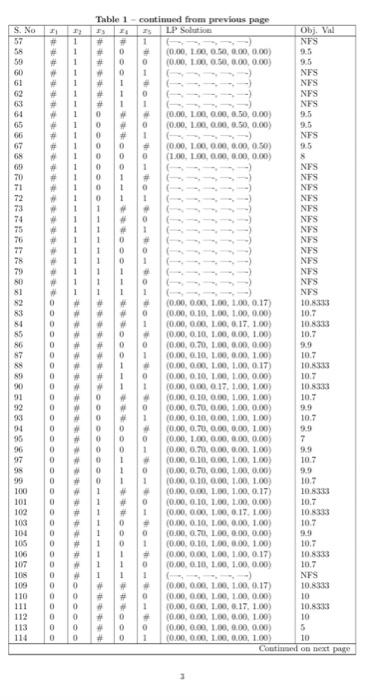
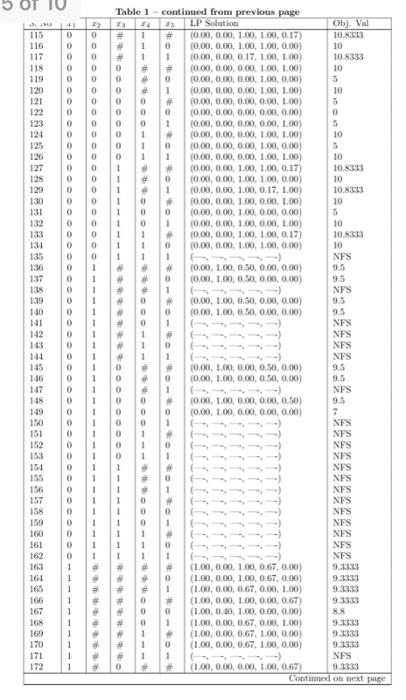
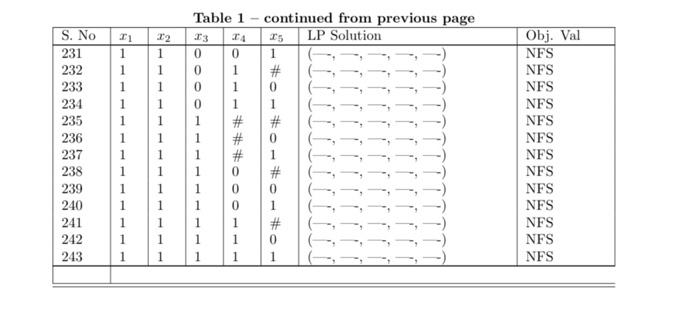
Consider the following IP problem. maximise:subjectto:x1+7x2+5x3+5x1+5x53x1+10x2+6x1+6x4+6x513xi{0,1}i=1,,5 (a) Write the LP relaxation of the above model. (b) Get the optimal objective function value of the L.P relackation from Table 1. Is it a lower or an upper bound? Explain. (c) Is x=[1,1,0,0,0t a feasible solution to the above problem. If yes, then obtain its objective function value from Table 1. Is it a lower or an upper bound? Explain. Solve the above problem using branch & bound mathod, and build the enumeration tree using the following strategies. You can use the information from Table 1. Note: Generute one tree for Part (d), one for Part (c) and one for Part (f). Druse inside cach node, the node number. Next to cach node write objoctire function salse and all the fractional cariables. Drase the branch down (or bounds) on the left side, and the branch sp (or ) Bounds on the right side. White generuting the tree, you should followe the strutegies as described. Dering the caccuthon of any struicyy, if the number of nodes processed is grrater than or epad to 20 , then you can termanate the strategy. Report the incumbent solation. Also, say in jercontage, how far it is from the best posvible nalution. For Strategy-1, werite the L.P formulation that unas solved at every 5th node. (d) Strategy-1: - Node Selection: Best First Select the node with the best objective function value. - Variable Selection: Nearest to integer A fractioual variable with fractiotal valoe nearost to an integer will be tased for branching. - Brasching Direction: Up Select the branch of side (lower bound is increased.) (e) Strategy-2: - Node Selection: Depth First the Best Back Select the most recently created child node to solve. If no child exists, then backtrack to the best bound node avillable in the entire tree. - Variable Selection: Lowrst fraction A fractional variable with lowost fraction will be used for branching. - Branching Direction: Down Select the branch of side (upper botasd is decreased.) (f) Strategy-3: - Node Selection: Breadth First the Best Next All nodes at one level of the search tree are proceased before any node at a deeper level. In a given kevel, best node should be processed first. - Variable Selection: Highest fraction A fractional variable with highest fraction will be used for branching. - Branding Direction: You are froe to pick any rale. Table 1 - coutiaued from previous page \begin{tabular}{|c|c|c|c|c|c|c|c|} \hline 5. No & x1 & x2 & x3 & x4 & x3 & LPS Solutive & Obj. Val \\ \hline 57 & # & 1 & \# & \# & 1 & (,,) & NFs \\ \hline 58 & \# & 1 & \# & 0 & # & (0.00,1.0,0.50,0.00,0.00) & 9.5 \\ \hline 59 & # & 1 & \# & 0 & 0 & (0.00,1.00,0.50,0.00,0.00) & 9.5 \\ \hline 60 & H & 1 & H & 0 & 1 & (,,) & NFS \\ \hline 61 & \# & 1 & # & 1 & & (,) & NFS \\ \hline 62 & \# & 1 & \# & 1 & 0 & (,,, & NFS \\ \hline 63 & \# & 1 & \# & 1 & 1 & (,,) & NFS \\ \hline 64 & H & 1 & 0 & \# & # & (0.00,1im,0.00,0.50,0.00) & 9.5 \\ \hline 65 & \# & 1 & 0 & \# & o & (0.00,1.00,0.00,0.50,0.00) & 9.5 \\ \hline 66 & # & 1 & 0 & \# & 1 & & NFS \\ \hline 67 & \# & 1 & 0 & 0 & # & (0.00,1.00,0.00,0.00,0.50) & 2.5 \\ \hline 68 & i & 1 & 0 & 0 & 0 & (1.00,1.00,0.00,0.00,0.00) & 8 \\ \hline 69 & \# & 1 & 0 & 0 & 1 & (,,) & NFS \\ \hline 70 & # & 1 & 0 & 1 & # & (,,) & NFS \\ \hline 71 & \# & 1 & 0 & t & a & (,,, & NFs \\ \hline 72 & * & 1 & 0 & 1 & 1 & & NFS \\ \hline 73 & H & 1 & 1 & \% & a & & NFS \\ \hline 74 & H & 1 & 1 & # & 0 & (,) & NFS \\ \hline 75 & \# & 1 & 1 & # & 1 & & NFS \\ \hline 76 & # & 1 & 1 & 0 & # & (,,,) & NFS \\ \hline 77 & * & 1 & 1 & 0 & 0 & & NFS \\ \hline 78 & \# & 1 & 1 & 0 & 1 & (,+,, & NFS \\ \hline 79 & \# & 1 & 1 & 1 & # & & NFS \\ \hline 80 & \# & 1 & 1 & 1 & 0 & (,,) & NFS \\ \hline 81 & i & I & 1 & 1 & 1 & (,,,,) & NPS \\ \hline 82 & 0 & # & \# & \# & # & (0.00,0.00.1.00,1.00,0.17) & 10.8353 \\ \hline 83 & 0 & & \# & # & a & (0.00,0.10,1.00,1.00,0.00) & 10.7 \\ \hline 84 & 0 & \# & \# & # & 1 & (0.00,0.00,1.00,0.17,1.00) & 10323 \\ \hline 85 & 0 & # & \# & 0 & & (0.00,0.10,1.00,0.00,1.00) & 10.7 \\ \hline 86 & 0 & # & \# & 0 & o & (0.00,0.70,1.00,0.00,0.00) & 29 \\ \hline 87 & 0 & \# & \# & 0 & 1 & (0.00,0.10,1.00,0.00,1.00) & 10.7 \\ \hline 88 & 0 & \# & \# & 1 & a & (0.00,0.00,1.00,1.00,0.17) & 10.833 \\ \hline 89 & 0 & \# & \# & 1 & o & (0.00,0.10,1.00,1.00,0.00) & 10.7 \\ \hline 90 & 0 & & & 1 & 1 & (0.00,0.00,0.17,1.00,1.00) & 10.8335 \\ \hline 91 & 0 & H & 0 & \# & H & (0.00,0.10,0.00,1.00,1.00) & 10.7 \\ \hline 92 & 0 & & 0 & & 0 & (0.00,0.70,0.00,1.00,0.00) & 9.9 \\ \hline 93 & 0 & # & 0 & # & 1 & (0.00,0.10,0.00,1.00,1.00) & 10.7 \\ \hline 94 & 0 & \# & 0 & 0 & a & (0.00,0.70,0.00,0.00,1.00) & 9.9 \\ \hline 95 & 0 & # & 0 & 0 & 0 & (0.00,1.00,0.00,0.00,0.00) & 7 \\ \hline 96 & 0 & & 0 & 0 & 1 & (0.00,0.70,0.00,0.00,1.00) & 9.9 \\ \hline 97 & 0 & # & 0 & 1 & H & (0.00,0.10,0.00,1.00,1.00) & 10.7 \\ \hline 98 & 0 & & 0 & 1 & 0 & (0.00,0.50,0.00,1.00,0.00) & 9.9 \\ \hline 99 & 0 & \# & 0 & 1 & 1 & (0.00,0.10,0.00,1.00,1.00) & 10.7 \\ \hline 100 & 0 & # & 1 & # & H & (0.90,0.00,1.00,1.00,0.17) & 10.8353 \\ \hline 101 & 0 & # & 1 & \# & 0 & (0.00,0.10,1.00,1.00,0.00) & 10.7 \\ \hline 102 & 0 & \# & 1 & # & 1 & (0.00,0.00,1.00,0.17,1.00) & 10.8393 \\ \hline 103 & 0 & # & 1 & 0 & # & (0.00,0.10,1.00,0.00,1.00) & 10.7 \\ \hline 104 & 0 & \# & 1 & 0 & 0 & (0.00,0.20,1.00,0.00,0.00) & 9.9 \\ \hline 105 & 0 & \# & 1 & 0 & 1 & (0.00,0.10,1.00,0.00,1.00) & 10.7 \\ \hline 106 & 0 & \# & 1 & 1 & # & (0.00,0.00,1.00,1.00,0.17) & 10.8333 \\ \hline 107 & 0 & # & 1 & 1 & a & (0.00,0.10,1.00,1.00,0.00) & 10.7 \\ \hline 108 & 0 & \# & 1 & 1 & 1 & (,,,, & NFS \\ \hline 100 & 0 & 0 & # & # & \# & (0.00,0.00,1.00,1.00,0.17) & 10.8333 \\ \hline 110 & 0 & 0 & \# & # & o & (0.00,0.00,1.00,1.00,0.00) & 10 \\ \hline 111 & 0 & 0 & H & \# & 1 & (0.00,0.00,1.00,0.17,1.00) & 10.8363 \\ \hline 112 & 0 & 0 & \# & 0 & \# & (0.00,0.00,1.00,0.00,1.00) & 10 \\ \hline 113 & 0 & 0 & # & 0 & 0 & (0.00,0.00,1.00,0.00,0.00) & 5 \\ \hline 114 & 0 & 0 & \# & 0 & 1 & (0.00,0.00,1.00,0.00,1.00) & 10 \\ \hline \end{tabular} Coutimaed on next page. 3 Table 1 - continued from nrevious nage Table 1: Optimal Solutions for All L.P Relaxations, \# Indicates Table 1 - continued from previous page \begin{tabular}{|c|c|c|c|c|c|c|c|} \hline 3,+ & +1 & x2 & x3 & x4 & x5 & L.P Solation & \\ \hline 115 & 0 & 0 & # & 1 & # & (0.00,0.00,1.00,1.00,0.17) & 10.8353 \\ \hline 116 & 0 & 0 & # & 1 & 0 & (0.00,0.00,1.00,1.00,0.00) & 10 \\ \hline 117 & 0 & 0 & \# & 1 & 1 & (0.00,0.00,0.17,1.00,1.00) & 10.8333 \\ \hline 118 & 0 & 0 & 0 & # & # & (0.00,0.00,0.00,1.00,1.00) & 10 \\ \hline 119 & 0 & 0 & 0 & 4 & 0 & (0.00,0.00,0.00,1.00,0.00) & 5 \\ \hline 120 & 0 & 0 & 0 & # & 1 & (0.00,0.00,0.00,1.00,1.00) & 10 \\ \hline 121 & 0 & 0 & 0 & 0 & # & (0.00,0.00,0.00,0.00,1.00) & 5 \\ \hline 122 & 0 & 0 & 0 & 0 & 0 & (0.00,0.00,0.00,0.00,0.00) & 0 \\ \hline 123 & 0 & 0 & 0 & 0 & 1 & (0.00,0.00,0.00,0.00,1.00) & 5 \\ \hline 124 & 0 & 0 & 0 & 1 & H & (0.00,0.00,0.00,1.00,1.00) & 10 \\ \hline 125 & 0 & 0 & 0 & 1 & 0 & (0.00,0.00,0.00,1.00,0.00) & 5 \\ \hline 126 & 0 & 0 & 0 & 1 & 1 & (0.00,0.00,0.00,1.00,1.00) & 10 \\ \hline 127 & 0 & 0 & 1 & iv & & (0.00,0.00,1.00,1.00,0.17) & 10.8333 \\ \hline 128 & 0 & 0 & 1 & # & 0 & (0.00,0.00,1.00,1.00,0.00) & 10 \\ \hline 129 & 0 & 0 & 1 & \# & 1 & (0.00,0.00,1.00,0.17.1.00) & 10.8343 \\ \hline 130 & 0 & 0 & 1 & 0 & \# & (0.00,0.00,1.00,0.00,1.00) & 10 \\ \hline 131 & 0 & 0 & 1 & 0 & 0 & (0.00,0.00,1.00,0.00,0.00) & 5 \\ \hline 132 & 0 & 0 & 1 & 0 & 1 & (0.00,0.00,1.00,0.00,1.00) & 10 \\ \hline 133 & 0 & 0 & 1 & 1 & \# & (0.00,0.00,1.00,1.00,0.17) & 10.8353 \\ \hline 134 & 0 & 0 & 1 & 1 & 0 & (0.00,0.00,1.00,1.00,0.00) & 10 \\ \hline 135 & 0 & 0 & 1 & 1 & 1 & (,,) & NFS \\ \hline 136 & 0 & 1 & # & \# & # & (0.00,1.00,0.50,0.00,0.00) & 9.5 \\ \hline 137 & 0 & 1 & \# & \# & 0 & (0.00,1.00,0.50,0.00,0.00) & 9.5 \\ \hline 138 & 0 & i & # & # & 1 & (,,,) & NFS \\ \hline 139 & 0 & i & \# & 0 & H & (0.00,1.00,0.50,0.00,0.00) & 9.5 \\ \hline 140 & 0 & 1 & H & 0 & 0 & (0.00,1.00,0.50,0.00,0.00) & 95 \\ \hline 141 & 0 & i & # & 0 & 1 & (,,,) & NFS \\ \hline 142 & 0 & i & \# & 1 & if & (,,, & NFS \\ \hline 143 & 0 & i & & 1 & 0 & (,,,) & NFS \\ \hline 144 & 0 & 1 & & 1 & 1 & (,,,) & NFS \\ \hline 145 & 0 & 1 & 0 & & ie & (0.00,1.00,0.00,0.50,0.00) & 9.5 \\ \hline 146 & 0 & 1 & 0 & & 0 & (0.00,1.00,0.00,0.50,0.00) & 95 \\ \hline 147 & 0 & 1 & 0 & 4 & 1 & (,,) & NFS \\ \hline 148 & 0 & i & 0 & 0 & & (0.00,1.00,0.00,0.00,0.50) & 95 \\ \hline 149 & 0 & i & 0 & 0 & 0 & (0.00,1.00,0.00,0.00,0.00) & 7 \\ \hline 150 & 0 & 1 & 0 & 0 & 1 & (,4,0) & NFS \\ \hline 151 & 0 & 1 & 0 & 1 & \# & (,,,,) & NFS \\ \hline 152 & 0 & 1 & 0 & i & 0 & (,,,, & NFS \\ \hline 153 & 0 & i & 0 & 1 & 1 & & NFS \\ \hline 154 & 0 & 1 & 1 & 4 & H & & NFS \\ \hline 155 & 0 & i & i & # & 0 & & NFS \\ \hline 156 & 0 & i & 1 & & 1 & (,,,,, & NFS \\ \hline 157 & 0 & i & i & 0 & H & (,,,, & NFS \\ \hline 158 & 0 & i & i & 0 & 0 & (,,, & NFS \\ \hline 159 & 0 & 1 & 1 & 0 & 1 & (,,,) & NFS \\ \hline 160 & 0 & 1 & 1 & 1 & # & (,,) & NFS \\ \hline 161 & 0 & 1 & 1 & 1 & 0 & (,,,) & NFS \\ \hline 162 & 0 & 1 & 1 & 1 & 1 & (,,,) & NFS \\ \hline 163 & 1 & # & \# & # & # & (1.00,0.00,1.00,0.67,0.00) & 9.2333 \\ \hline 164 & 1 & 4 & \# & H & 0 & (1.00,0.00,1.00,0.67,0.00) & 9.3339 \\ \hline 165 & 1 & # & # & # & 1 & (1.00,0.00,0.67,0.00,1.00) & 9.3333 \\ \hline 166 & 1 & \# & \# & 0 & \# & (1.00,0.00,1.00,0.00,0.6) & 9.3333 \\ \hline 167 & 1 & , & \# & 0 & 0 & (1.00,0.40,1.00,0.00,0.00) & 8.8 \\ \hline 168 & 1 & # & # & 0 & 1 & (1.00,0.00,0.67,0.00,1.00) & 93333 \\ \hline 169 & 1 & \% & & 1 & & (1.00,0.00,0.67,1.00,0.00) & 9.3333 \\ \hline 170 & 1 & \# & # & 1 & 0 & (1.00,0.00,0.67,1.00,0.00) & 9.3333 \\ \hline 171 & 1 & # & # & 1 & 1 & & NFS \\ \hline 172 & 1 & # & 0 & # & # & (1.00,0.00,0.00,1.00,0.67) & 93333 \\ \hline \end{tabular}