Please solve

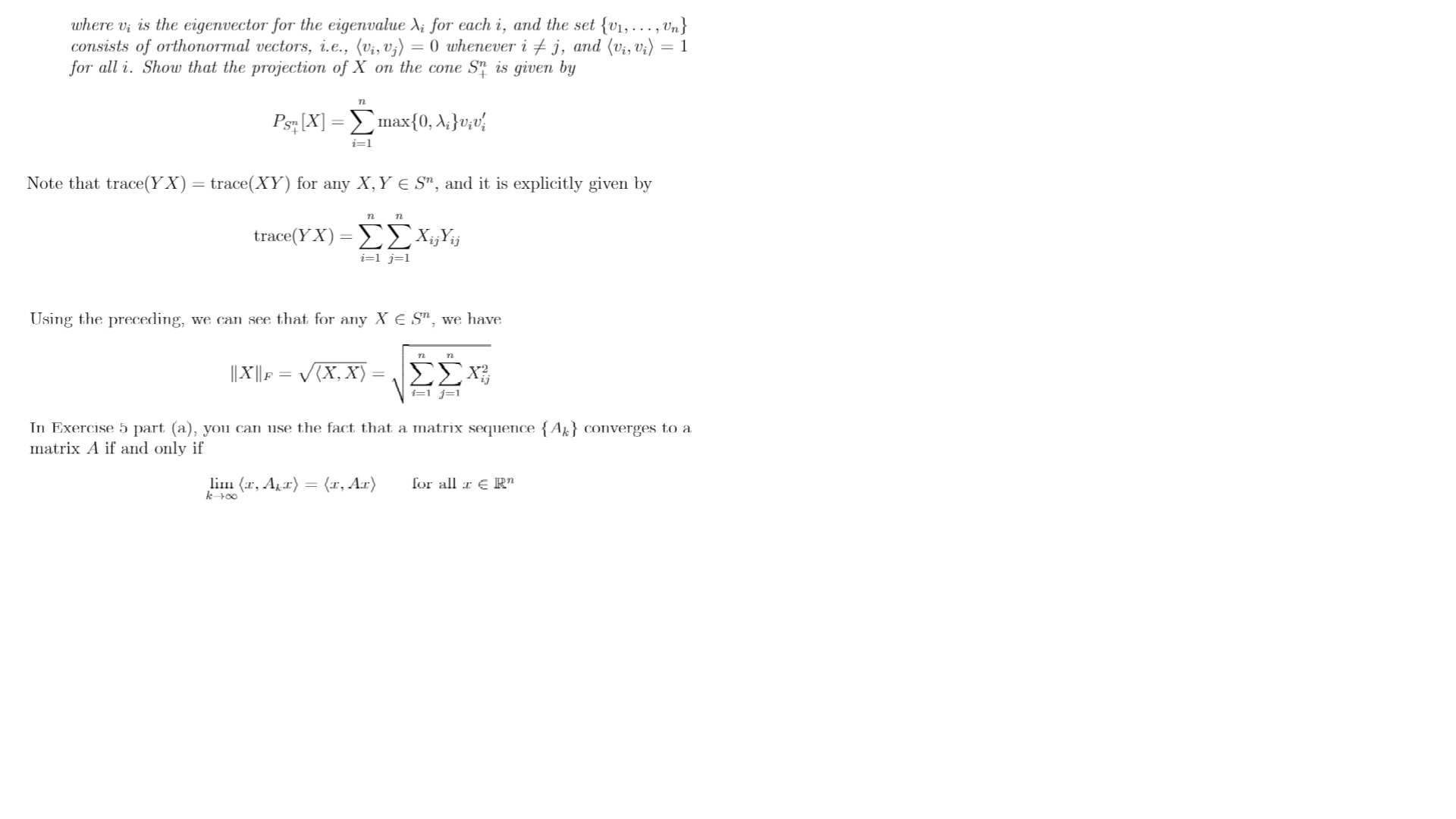
where vi is the eigenvector for the eigenvalue di for each i, and the set {v1, . . . , Un} consists of orthonormal vectors, i.e., (vi, v;) = 0 whenever i f j, and (vi, vi) = 1 for all i. Show that the projection of X on the cone ST is given by Ps. [X] = max {0, A; }viv; 1= 1 Note that trace(Y X) = trace(XY) for any X, Y E S", and it is explicitly given by trace(Y X) = _ _ Xij Yui i=1 j=1 Using the preceding, we can see that for any X c S", we have [IX|F = V(X, X) = EEX In Exercise 5 part (a), you can use the fact that a matrix sequence { Ax } converges to a matrix A if and only if lim (x, AT) = (x, Ar) for all a e InWe will consider the space of symmetric n x n matrices, denoted by S. The inner product of two matrices X and Y in S" is defined by (Y, X) = trace(Y X). We will also consider the matrix norm induced by this inner product, which is the Frobe- nius norm, given by IX IF = V(X, X) Let ST denote the set of all n x n positive semidefinite symmetric matrices. (a) Show that ST is a closed conver cone. (b) Show that the cone ST is self-dual, i.e., (Sn)* = Sn (c) Let X E S" have the eigenvalue decomposition n