Please solve with steps.

P.S. The general formulas for divergence and curl in curvilinear coordinates are attached for reference.

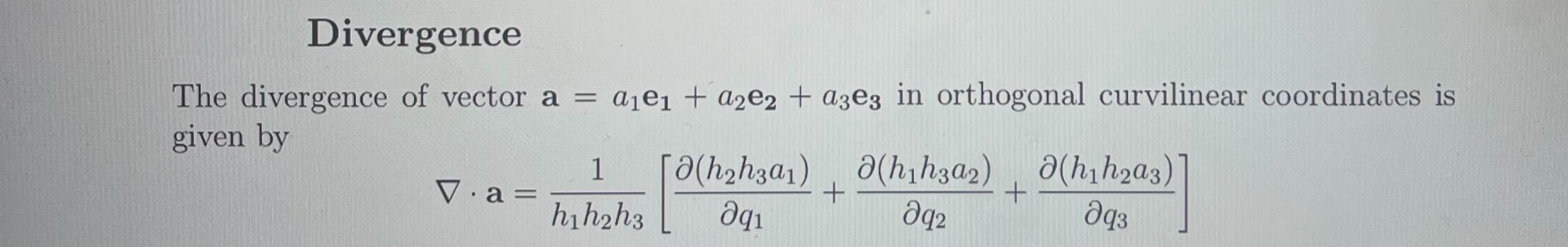
2. Consider the spherical polar coordinates (r, 0, 4) with unit vectors er, eo, ey (a) Find the expressions of the unit vectors er, es, ex as functions of (r, 0, 4) with respect to the Cartesian unit vectors i, j, k. (b) Using the expressions derived above, show that er, es and ey are mutually orthogonal and further that er X eo = ey. (c) Using the general formulas for divergence and curl in curvilinear coordinates from the lectures, write the expressions for the divergence and curl of a vector V = Vrer + Veee + Upey in spherical polar coordinates. You can leave the expression for curl in determinant form. (d) Hence find the divergence and curl of the vector v = r sin 0 sin per + rep.Divergence The divergence of vector a = ale1 + 02e2 + age3 in orthogonal curvilinear coordinates is given by 1 (h2h3a1) a(h1h3a2) a(h1h2a3) + V . a= + 293 hih2h3 aq1 292Curl The curl of vector a = ale1 + age2 + age3 in orthogonal curvilinear coordinates is given by e3 da da da e1 e2 x X X h2 2q2 h3 293 Vxa = h1 aq1 1 dazh2 dajh1 e3 dajh1 da3h3 1 e2+ aq1 2q2 hih2 dagh3 aazh2 e1 + hih3 hzh3 2q2 2q3 This can be written as he hze2 h3e3 a a aq2 2q3 Vxa= 2q1 hihzh3 hial h2a2 h3a3