Please turn the following algorithm into a C++ program.

Part 1: Implement the stack traversal for the pseudocode template given below, and produce identical output (stack traversal path and the tree array). Traverse Graph 1 and USE NODE C as the ROOT.

Part 2: Modify your implementation to traverse GRAPH 2 shown below. USE NODE A as the ROOT. Output the stack traversal path and the tree array.

// A recursive solution for a stack traversal of a graph

/* Each instance of traverse keeps track of one nodes adjacency list. The CALL to and RETURN from traverse, are similar to PUSH and POP.

FYI: This code began its life in C#, mkay? */ 

// the graph adjacency matrix 

static int[,] graph = { {0,1,1,0,0,0,0,0}, //A {1,0,1,0,0,0,0,0}, //B {1,1,0,1,0,1,0,0}, //C {0,0,1,0,1,0,0,0}, //D {0,0,0,1,0,1,0,0}, //E {0,0,1,0,1,0,1,1}, //F {0,0,0,0,0,1,0,0}, //G {0,0,0,0,0,1,0,0}, //H 

//A B C D E F G H

};

// where I've been 

static bool[] visited = {false, false, false, false, false, false, false, false};

// the resulting tree. Each node's parent is stored

static int[] tree = {-1, -1, -1, -1, -1, -1, -1, -1}; 

static void Main() { 

// "Push" C

 traverse(2); 

 printtree(); } 

void traverse(node) { 

 mark node as visited print(node) 

init target to 0 // index 0 is node A while(not at end of nodes list) // count thru cols in nodes row

{

if(target is nodes neighbor and target is unvisited)

{

 mark that targets parent is node 

 traverse(target) // this is like a push } 

next target

}

 return // this is like a pop } 

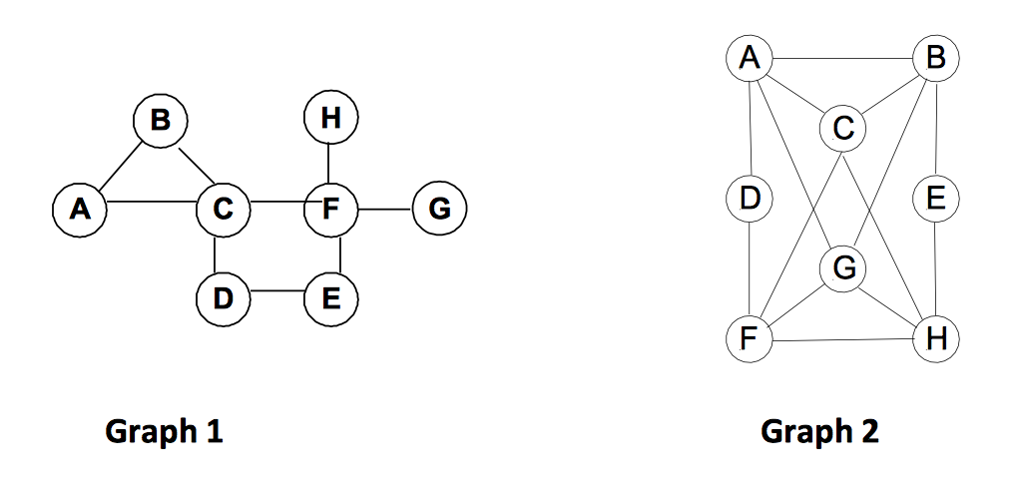
B H C A D (G D E F Graph 1 Graph 2 E (C)1111( )