please TYPE out the answers & BOLD them. no handwritten!

THIS IS ALL THE INFORMATION PROVIDED FOR THIS QUESTION

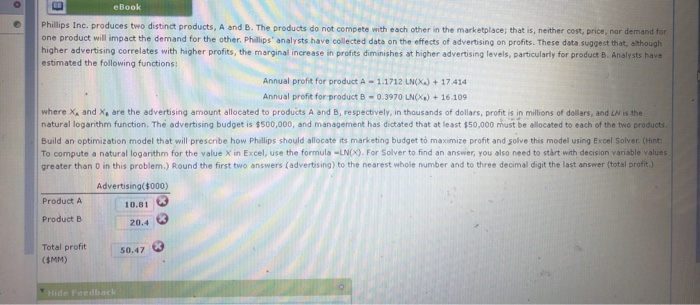
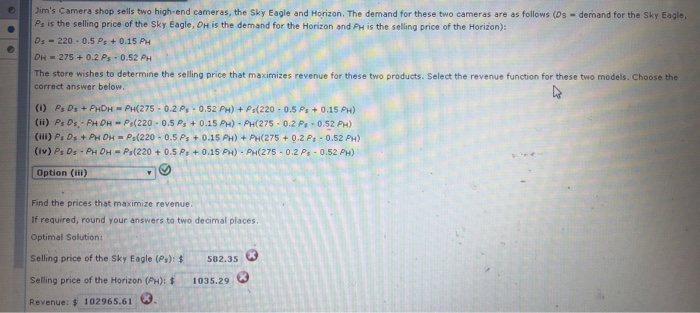
Jim's Camera shop sells two high-end cameras, the Sky Eagle and Horizon. The demand for these two cameras are as follows (Ds - demand for the Sky Eagle, Ps is the selling price of the Sky Eagle, Dw is the demand for the Horizon and P is the selling price of the Horizon): Ds - 220 -0.5 Ps+0.15 4 DH=275 +0.2 Ps - 0.52 PH The store wishes to determine the selling price that maximizes revenue for these two products. Select the revenue function for these two models. Choose the correct answer below. (1) PsDs + PHDH - PH(275.0.2 P: 0.52 P.) + Ps(220 - 0.5 Ps+0.15 PH) (ii) Ps Ds.PH DH-P(220 -0.5 P, +0.15 PH) - PH(275.0.2 P3 -0.52 P.) (all) P: Ds + PHDH = Ps(220 - 0.5 Ps+0.15 PH) + PH(275+ 0.2 P: -0.52 PH) (iv) Ps D - H OH = P (820 + 05 P + 0,15 FH) - PH 275 - 0,2 Ps - 0.52 PM) Option (11) Find the prices that maximize revenue If required, round your answers to two decimal places Optimal Solution: Selling price of the Sky Eagle (Ps): $ 582.35 Selling price of the Horizon (PO$ 1035.29 3 Revenue: $ 102965.61 . ebook Phillips Inc. produces two distinct products, A and B. The products do not compete with each other in the marketplace that is neither cost, price, nor demand for one product will impact the demand for the other. Phillips' analysts have collected data on the effects of advertising on profits. These data suggest that although higher advertising correlates with higher profits, the marginal increase in profits diminishes at higher advertising levels, particularly for product B. Analysts have estimated the following functions: Annual profit for product A - 1.1712 LN(X) + 17 414 Annual profit for product B -0.3970 LN(X) + 16.109 where X, and X, are the advertising amount allocated to products A and B, respectively, in thousands of dollars, profit is in millions of dollars, and LN is the natural logarithm function. The advertising budget is $500,000, and management has dictated that at least $50,000 must be allocated to each of the two products, Build an optimization model that will prescribe how Phillips should allocate its marketing budget to maximize profit and solve this model using Excel Solver (Hint: To compute a natural logarithm for the value X in Excel, use the formula LN(X). For Solver to find an answer, you also need to start with decision variable values greater than 0 in this problem.) Round the first two answers (advertising) to the nearest whole number and to three decimal digit the last answer (total profit) Advertising (5000) Product A 10.813 Product B 20. 43 Total profit (SMM) 50.47 03 Hide feedback