Please use Excel

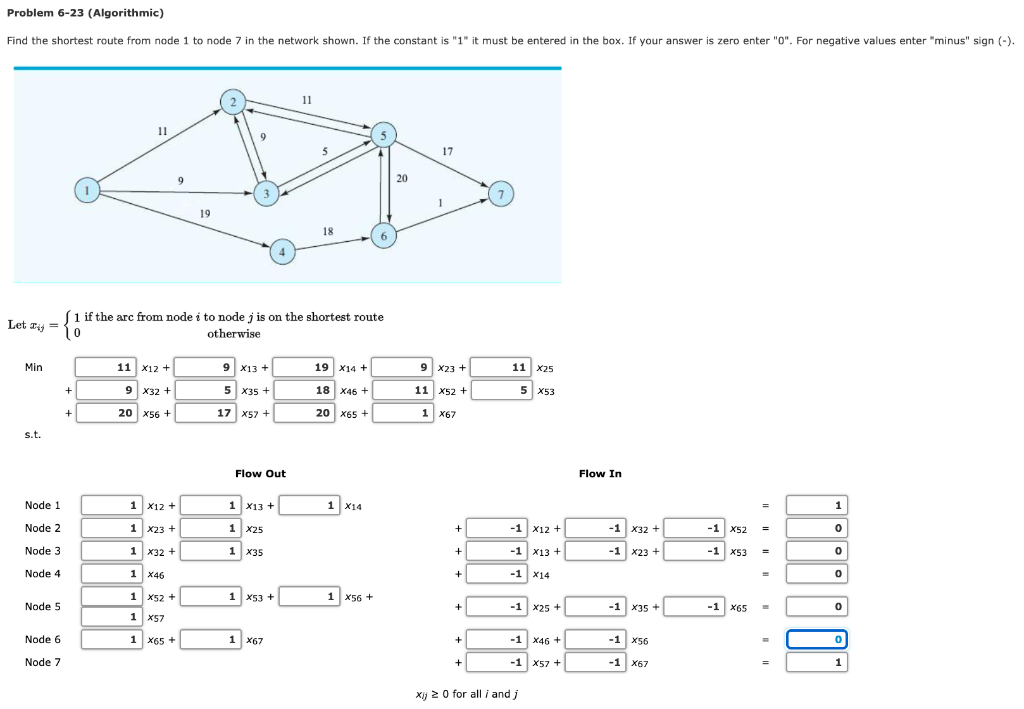
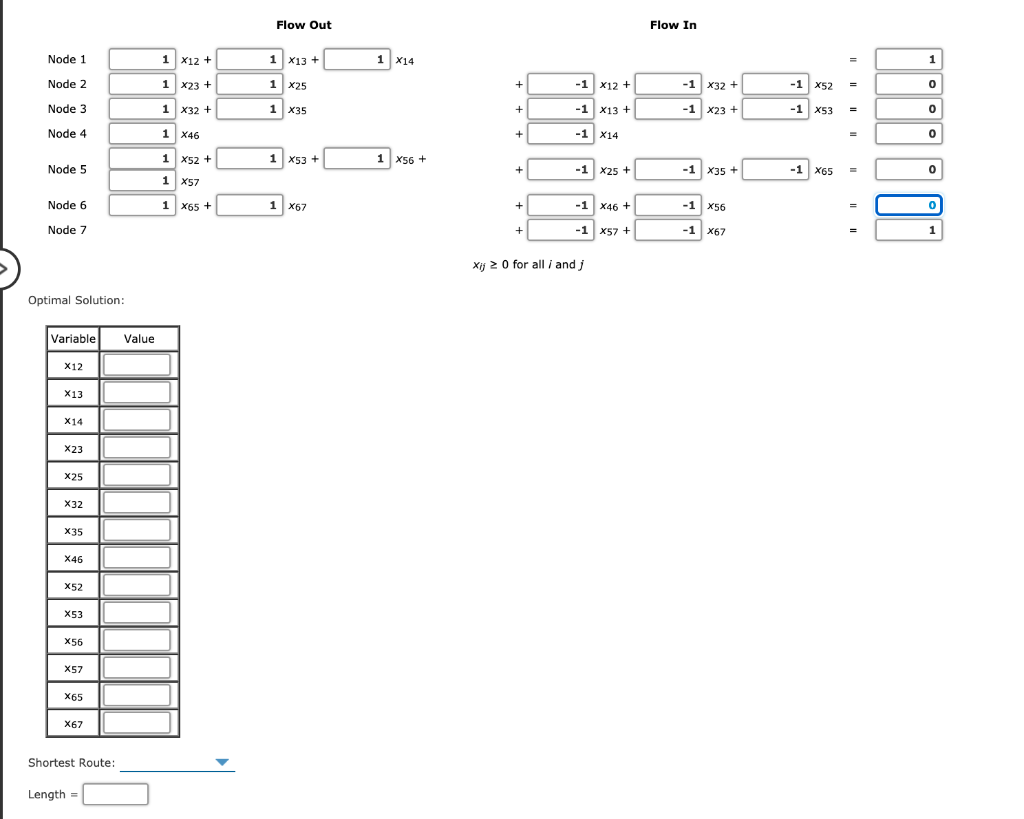
Problem 6-23 (Algorithmic) Find the shortest route from node 1 to node 7 in the network shown. If the constant is "1" it must be entered in the box. If your answer is zero enter "O". For negative values enter "minus" sign (-). 11 11 9 5 17 9 20 19 18 if the arc from node i to node j is on the shortest route Let y = 10 otherwise Min 11 X12 + 9 X13 + 19 X14 + 9 X23 + 11 25 9 X32 + 5 X35 + 18 146 + 11 x52 + 5 X53 + + 20 x56 + 17 X57 + 20 X65 + 1 X67 s.t. Flow Out Flow In Node 1 1 X12 + 1 *13+ 1 X14 1 Node 2 1 1 X23 + 1 x25 + -1 X12 + -1 X52 = o -1 x32 + -1 X23 + Node 3 1 x32 + 1 X35 + -1 X13 + -1 X53 o Node 4 1 X46 + -1 X14 o 1 x52 + 1 X53 + 1 X56 + 1 Node 5 + -1 x25 + -1 X35 + -1 X65 0 1 X57 Node 6 1 X65 + 1 X67 + -1 X46 + -1 X56 0 Node 7 + -1 X57 + -1 X67 1 Xij 20 for all i andj Flow Out Flow In Node 1 1 X12 + 1 X13 + 1 X14 1 Node 2 1 X23 + 1 x25 + -1 X12 + o 0 -1 x32 + -1 X23+ -1 X52 -1 X53 Node 3 1 x32 + 1 X35 + -1 X13 + 0 Node 4 1| X46 + -1 X14 o 1 X52 + 1 X53 + 1 X56 + Node 5 + + -1 x25 + -1 X35 + -1 X65 o 1 X57 Node 6 1 X65 + 1 X67 + -1 146 + -1 X56 0 Node 7 + -1 X57 + -1 X67 = 1 Xij 2 0 for all i andj Optimal Solution: Variable Value X12 X13 X14 X23 X25 X22 X35 X46 X52 X53 X56 X57 X65 X67 Shortest Route: Length =