Please use MATLAB to solve this problem.

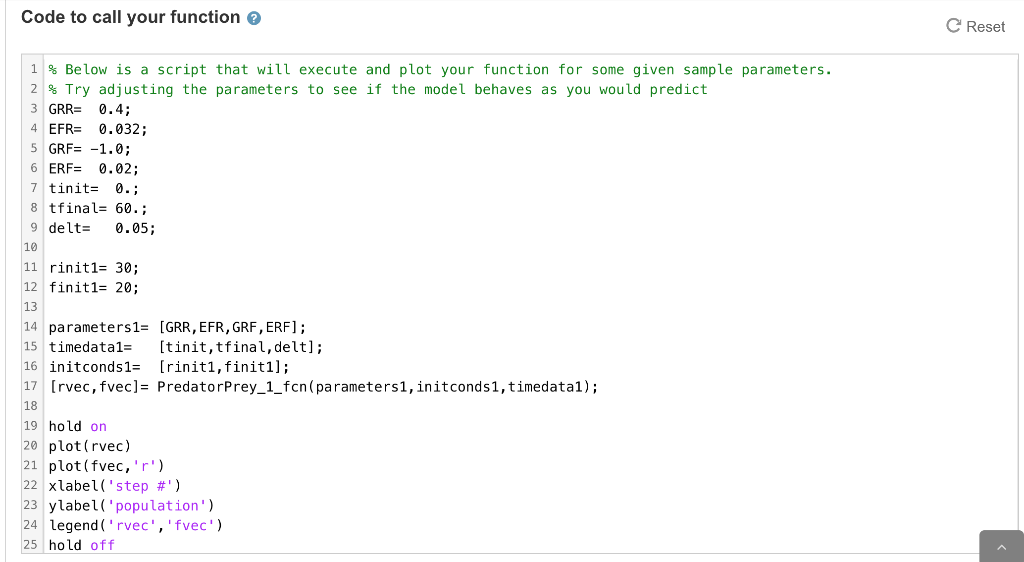
Case 1: Base Case Model Investigate effects of initial conditions (rinit,finit) on r(t) and f(t) populations. This is the basic system as outlined in the class lecture. Governing equations, inputs and outputs are described in detail below. o O Governing Equations: dr/dt = GRR*r -(EFR*f)*r r, rabbits df/dt = GRF*f +(ERF*r)*f f, foxes t = time, in years Inputs parameters= (GRR,EFR, GRF, ERF] o GRR, growth rate of rabbits EFR, effect of foxes on rabbit increase GRF, growth rate of foxes ERF, effect of rabbits on fox increase initconds=[rinit,finit] rinit, initial rabbit population finit, initial fox population timedata= [tinit,tfinal,delt] 0 nit, time at the start of the model run tfinal, time at the end of the model run delt, the size of the time step in Euler's method Outputs rvec, rabbit history fvec, fox history O O O o Function Setup function (rvec,fvec]=Predator Prey_1_fcn(parameters,initconds,timedata) % Your code here end Test Case 1 O solutions submitted (max: 4) Enter your function from Test Case 1 into the space below. Click the run button to test your code output using the provided script Click the submit button to have your work assessed. You have a 4 submission limit. Function C Reset MATLAB Documentation 1 function [rvec, fvec]=PredatorPrey_1_fcn(parameters, initconds, timedata) 2 % Copy and paste your code here 3 4 end Code to call your function C Reset 1 % Below is a script that will execute and plot your function for some given sample parameters. 2 % Try adjusting the parameters to see if the model behaves as you would predict 3 GRR= 0.4; 4 EFR= 0.032; 5 GRF= -1.0; 6 ERF= 0.02; 7 tinit= 0.; 8 tfinal= 60.; 9 delt= 0.05; 10 11 rinit1= 30; 12 finit1= 20; 13 14 parameters1= [GRR, EFR, GRF, ERF]; 15 timedatal= [tinit,tfinal, delt]; 16 initconds1= [riniti, finit1]; 17 [rvec, fvec)= Predator Prey_1_fcn(parametersi, initconds1, timedatai); 18 19 hold on 20 plot(rvec) 21 plot(fvec,'r') 22 xlabel('step #') 23 ylabel('population') 24 legend('rvec','fvec') 25 hold off