Please use python 3 thanks!

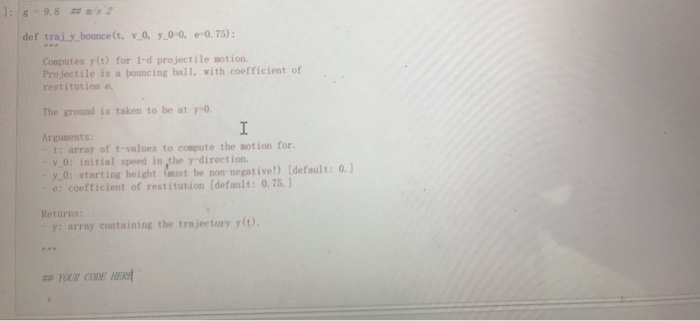
Part C (8 points) Alright, lumps of clay are still pretty boring. A much more interesting version of this problem is to simulate the motion of a bouncing ball, which will flty up into the air again once it hits the ground The simplest way to model a bouncing ball is using the coefficient of restitution e, which is equal to the ratio of incoming to outgoing speed when the ball bounces. For example, a tennis ball with e 0.75 that hits the ground at 4 m/s will bounce back up with a speed of 3 m/s-after which it obeys the same simple equation of motion as above. Implement a new function bounce y(t, v 0, e) that will produce the trajectory of a bouncing ball. (Hint: the art of this solution is all in finding a good algonithm! My suggestion is the following, which is nicely adapted to a ahile loop) Start by calculating the full y(0) without bouncing, letting y go negative Now, look for where the current trajectory y is negative: that entire part of the trajectory should be replaced by a new trajectory that starts with a bounce The starting speed of the bounce is equal td he ending speed of the previous trajectory, times the coefficient of restitution e. You could calulate v() there's a very simple relation between the initial and final speeds due to energy conservation-remember, energy is still conserved in between bounces Repeat the steps above until there are no negative y values left The p any 0 function will definitely come in handy for your while loop. For replacing only the negative part of y. you'll need a mask- and remember, whern to a mask of an array almask] b, the array b had better be the same length as almask1 Part C (8 points) Alright, lumps of clay are still pretty boring. A much more interesting version of this problem is to simulate the motion of a bouncing ball, which will flty up into the air again once it hits the ground The simplest way to model a bouncing ball is using the coefficient of restitution e, which is equal to the ratio of incoming to outgoing speed when the ball bounces. For example, a tennis ball with e 0.75 that hits the ground at 4 m/s will bounce back up with a speed of 3 m/s-after which it obeys the same simple equation of motion as above. Implement a new function bounce y(t, v 0, e) that will produce the trajectory of a bouncing ball. (Hint: the art of this solution is all in finding a good algonithm! My suggestion is the following, which is nicely adapted to a ahile loop) Start by calculating the full y(0) without bouncing, letting y go negative Now, look for where the current trajectory y is negative: that entire part of the trajectory should be replaced by a new trajectory that starts with a bounce The starting speed of the bounce is equal td he ending speed of the previous trajectory, times the coefficient of restitution e. You could calulate v() there's a very simple relation between the initial and final speeds due to energy conservation-remember, energy is still conserved in between bounces Repeat the steps above until there are no negative y values left The p any 0 function will definitely come in handy for your while loop. For replacing only the negative part of y. you'll need a mask- and remember, whern to a mask of an array almask] b, the array b had better be the same length as almask1