please use r studio

You are playing a game with two dice, according to the following rules:

In the first roll, if the total of the dice is 2, 3, or 12, you lose the game. In the first roll, if the total of the dice is 7 or 11, you win the game. For any other outcome, roll the dice again. If you get the same outcome again, you win. If you get a 7, you lose. Otherwise, repeat rolling the dice until you win or lose. To win after the second roll, you must get the outcome right before this one. Example games:

Roll 7. Win after a single roll. Roll 3. Loss after a single roll. Roll 5. Roll a 7. Loss after two rolls. Roll a 5. Roll a 4. Roll a 4. Win after three rolls. Roll a 8. Roll a 6. Roll a 8. Roll a 7. Loss after four rolls. Most games end after a small number of rolls, but there is a small probability of seeing arbitrarily large number of rolls until a game ends.

We will simulate this game of dice with random-number generators: Roll two dice as many times as needed, run the game until it ends, and store the number of rolls until the game has ended.

Write a function named gamecounts(ngames) that will play this game ngames times, and returns a vector such that the i-th element gives the count of games that ended after i rolls, up to 30 rolls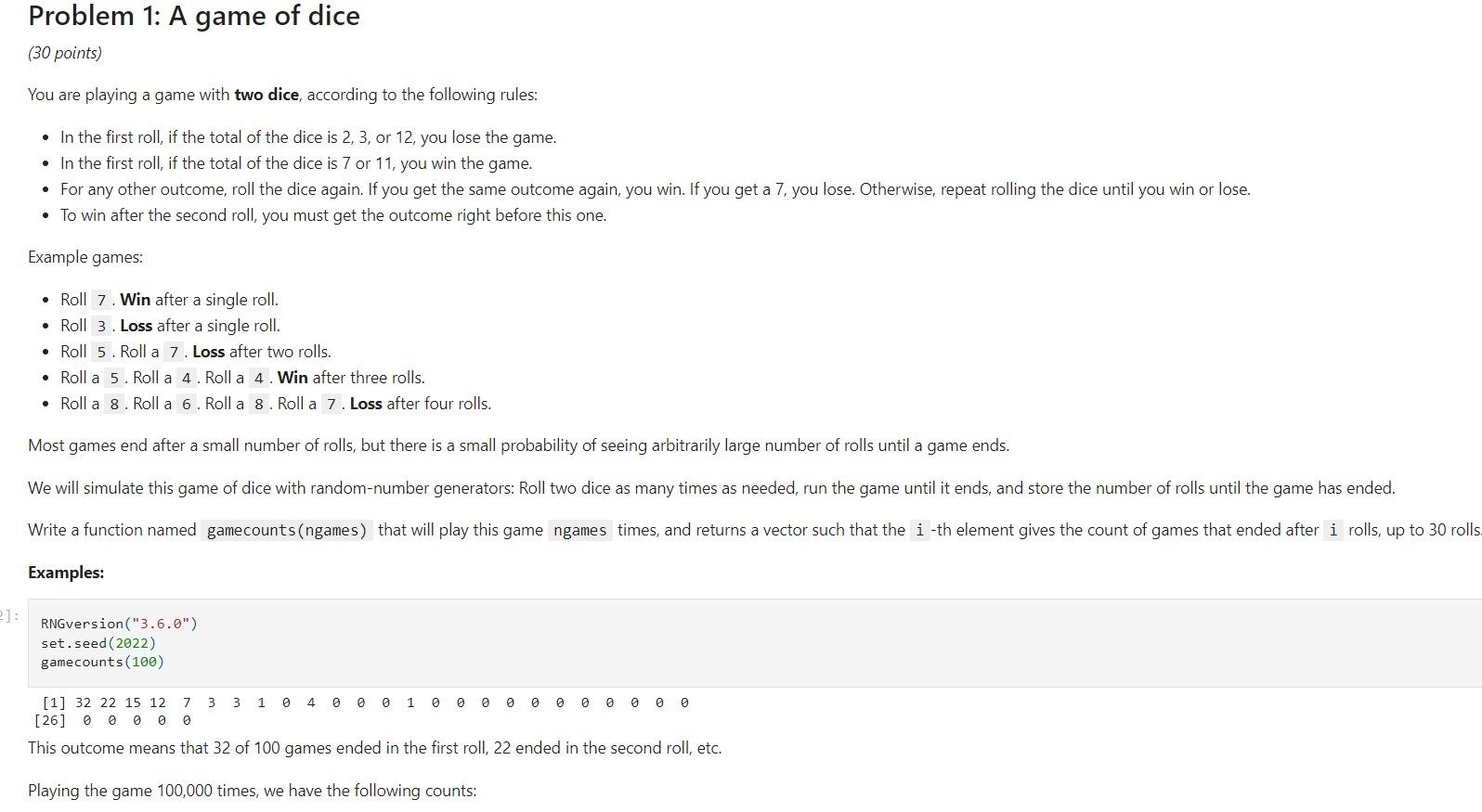

Problem 1: A game of dice (30 points) You are playing a game with two dice, according to the following rules: In the first roll, if the total of the dice is 2, 3, or 12, you lose the game. In the first roll, if the total of the dice is 7 or 11, you win the game. For any other outcome, roll the dice again. If you get the same outcome again, you win. If you get a 7, you lose. Otherwise, repeat rolling the dice until you win or lose. To win after the second roll, you must get the outcome right before this one. Example games: Roll 7. Win after a single roll. Roll 3. Loss after a single roll. Roll 5. Roll a 7. Loss after two rolls. Roll a 5. Roll a 4. Roll a 4. Win after three rolls. Roll a 8. Roll a 6. Roll a 8. Roll a 7. Loss after four rolls. Most games end after a small number of rolls, but there is a small probability of seeing arbitrarily large number of rolls until a game ends. We will simulate this game of dice with random-number generators: Roll two dice as many times as needed, run the game until it ends, and store the number of rolls until the game has ended. Write a function named gamecounts(ngames) that will play this game ngames times, and returns a vector such that the i-th element gives the count of games that ended after i rolls, up to 30 rolls Examples: 2]: RNGversion ("3.6.0") set.seed (2022) gamecounts (100) 0 0 0 [1] 32 22 15 12 7 3 3 1 4 0 0 0 1 0 0 0 [26] 0 0 0 0 This outcome means that 32 of 100 games ended in the first roll, 22 ended in the second roll, etc. Playing the game 100,000 times, we have the following counts