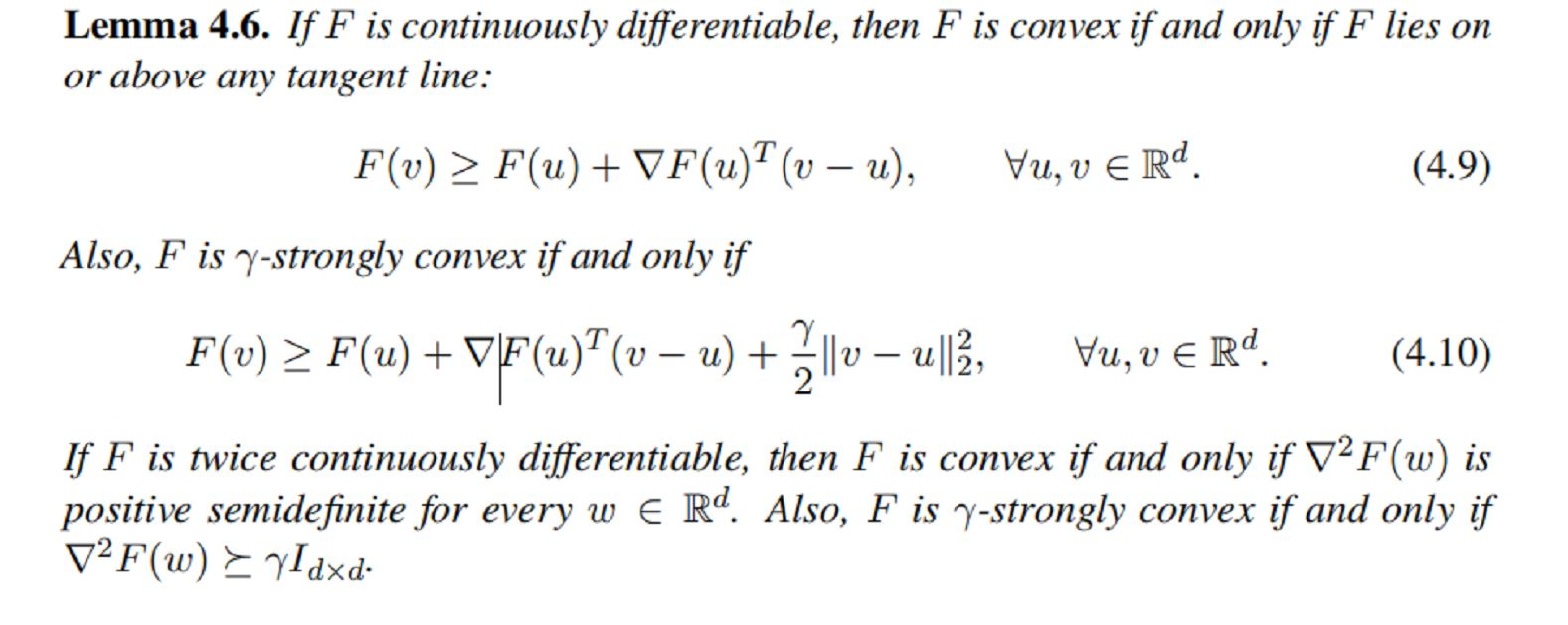
Please use the hint!

Question 1 (5 marks). Prove the strongly convex case of Theorem 4.9: Suppose F is 7-strongly convex and L-smooth with minimizer w*, and we run gradient descent (Wk+1 = wk akVF(wk)) with ak = 1/L starting from any wo E Rd. Show that F(wk) F(w*) 0. Hint: first show that F(w*) > F(w) Z || 1F(w) ||for all w by minimizing each side of (4.10) with respect to v. Lemma 4.6. If F is continuously differentiable, then F is convex if and only if F lies on or above any tangent line: F(v) > F(u) + VF(u)? (v u), Vu, 06 Rd. (4.9) Also, F is y-strongly convex if and only if F(v) > F(u) + VF(u)"(v u) + 2llo u|3; Vu, ve Rd. (4.10) If F is twice continuously differentiable, then F is convex if and only if V2F(w) is positive semidefinite for every w E Rd. Also, F is y-strongly convex if and only if V2F(w) yIdxd Gradient Descent The simplest optimization algorithm is called gradient descent (or steepest descent). Intuitively, we note that: If VF(w)T's > 0, then s is (locally) a direction of increasing F (that is, F(w + as) > F(w) for a > 0 sufficiently small); If VF(w)?s = 0, then s is a direction of constant F; and If VF(w)Is 0 (representing the fact that - VF(w) is only the best direction locally, not globally). The simplest choice of step sizes is as = 1/L for all k (when F is L-smooth). In that case, we use (4.12) and (4.8) to obtain F(wk 04 VF(wk)) 0. Hint: first show that F(w*) > F(w) Z || 1F(w) ||for all w by minimizing each side of (4.10) with respect to v. Lemma 4.6. If F is continuously differentiable, then F is convex if and only if F lies on or above any tangent line: F(v) > F(u) + VF(u)? (v u), Vu, 06 Rd. (4.9) Also, F is y-strongly convex if and only if F(v) > F(u) + VF(u)"(v u) + 2llo u|3; Vu, ve Rd. (4.10) If F is twice continuously differentiable, then F is convex if and only if V2F(w) is positive semidefinite for every w E Rd. Also, F is y-strongly convex if and only if V2F(w) yIdxd Gradient Descent The simplest optimization algorithm is called gradient descent (or steepest descent). Intuitively, we note that: If VF(w)T's > 0, then s is (locally) a direction of increasing F (that is, F(w + as) > F(w) for a > 0 sufficiently small); If VF(w)?s = 0, then s is a direction of constant F; and If VF(w)Is 0 (representing the fact that - VF(w) is only the best direction locally, not globally). The simplest choice of step sizes is as = 1/L for all k (when F is L-smooth). In that case, we use (4.12) and (4.8) to obtain F(wk 04 VF(wk))