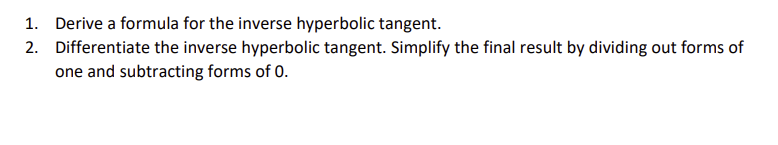
Please using this example:

NOTE: THE FIRST TWO IMAGES ARE THE EXAMPLES

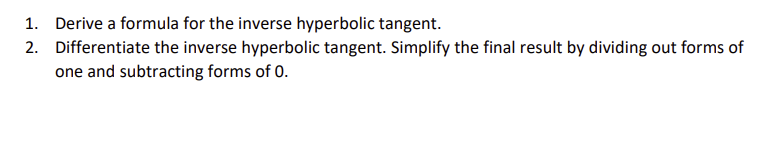
5.4.1 Derive Inverse Hyperbolic Sine x -sinh y. ey - ey 2 ed - ey ey 2 py e2y 2ey 2xey -e29 - 1. e2y - 2xey - 1=0. u2 - 2xu - 1=0. u =- -(-2a) + V (-2x)2 - 4(1) (-1) 2(1) 2x + V4x2+4 2 2x + 2va2 + 1 2 =atva'+1. ey =x+Vx2+1. In(ey) =In(ac + Vac2 + 1). y =In(ac + Vac2 + 1).Why was the :I: left out of the quadratic solution? Because e?"r is always positive, so that would not provide a real solution for us. y:1n(:n + V 3:2 + 1). _ 1 _ 13:2 1f2 :1: \"Hm (\"5 +1) (2)) _ l +11:(:1:2 + 1)_1f2 a: +V$2+ 1 _ l +II:(:E2 + 1)_1'l2 39+ 1 m+V32+1 Vm2+1 V$2+1+$ =(m+\\/mz+1)m 1 m2+1. Notice in what ways this is similar to the derivative of inverse sine function and in which ways it is different. 1. Derive a formula for the inverse hyperbolic tangent. 2. Differentiate the inverse hyperbolic tangent. Simplify the final result by dividing out forms of one and subtracting forms of 0