Please view problem

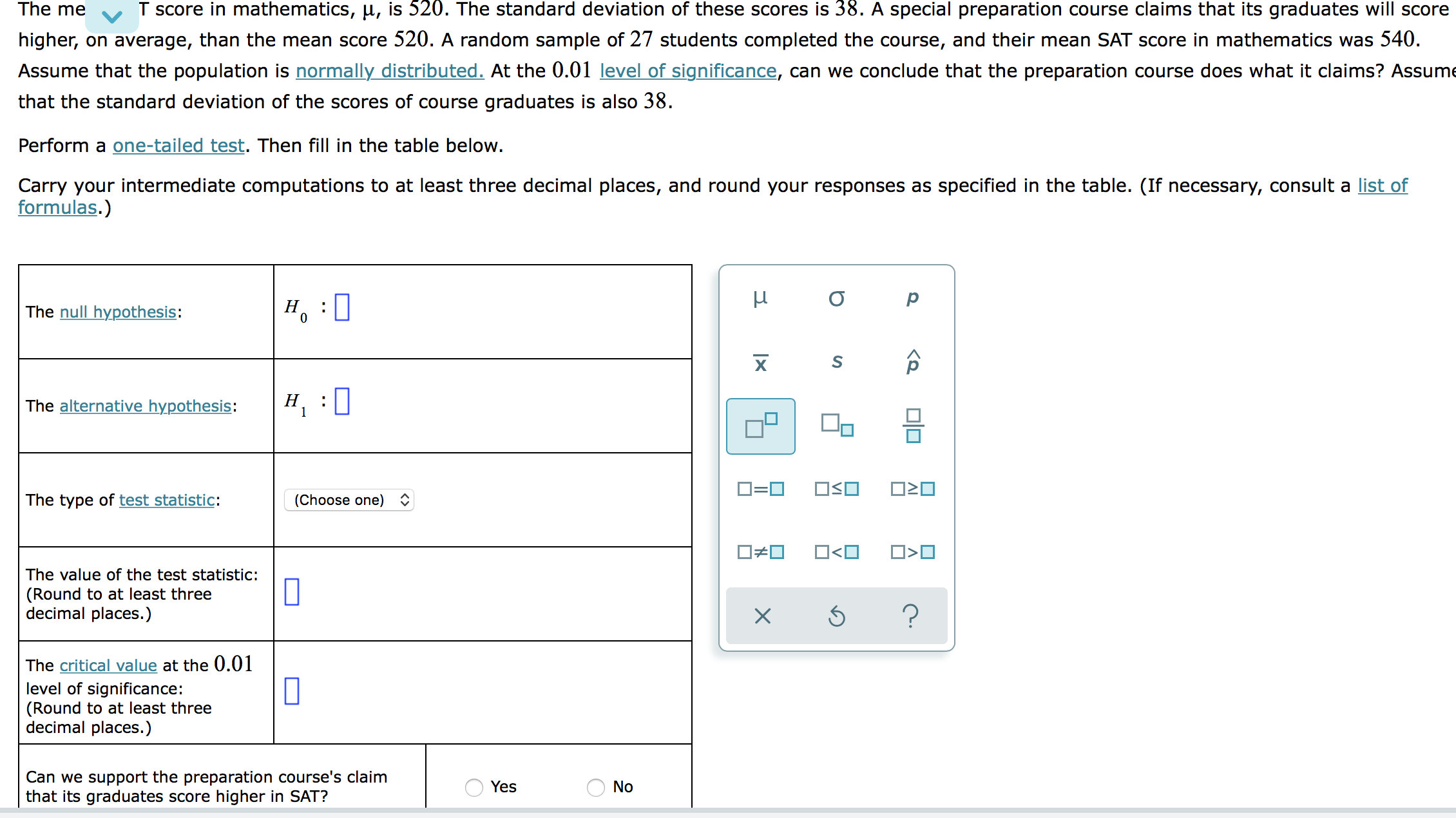
The me T score in mathematics, u, is 520. The standard deviation of these scores is 38. A special preparation course claims that its graduates will score higher, on average, than the mean score 520. A random sample of 27 students completed the course, and their mean SAT score in mathematics was 540. Assume that the population is normally distributed. At the 0.01 level of significance, can we conclude that the preparation course does what it claims? Assum that the standard deviation of the scores of course graduates is also 38. Perform a one-tailed test. Then fill in the table below. Carry your intermediate computations to at least three decimal places, and round your responses as specified in the table. (If necessary, consult a list of formulas.) The null hypothesis: H : H O P X S p The alternative hypothesis: H : The type of test statistic: (Choose one) 0=0 030 020 0*0 00 The value of the test statistic: (Round to at least three decimal places.) X 5 ? The critical value at the 0.01 level of significance: (Round to at least three 0 decimal places.) Can we support the preparation course's claim that its graduates score higher in SAT? Yes No