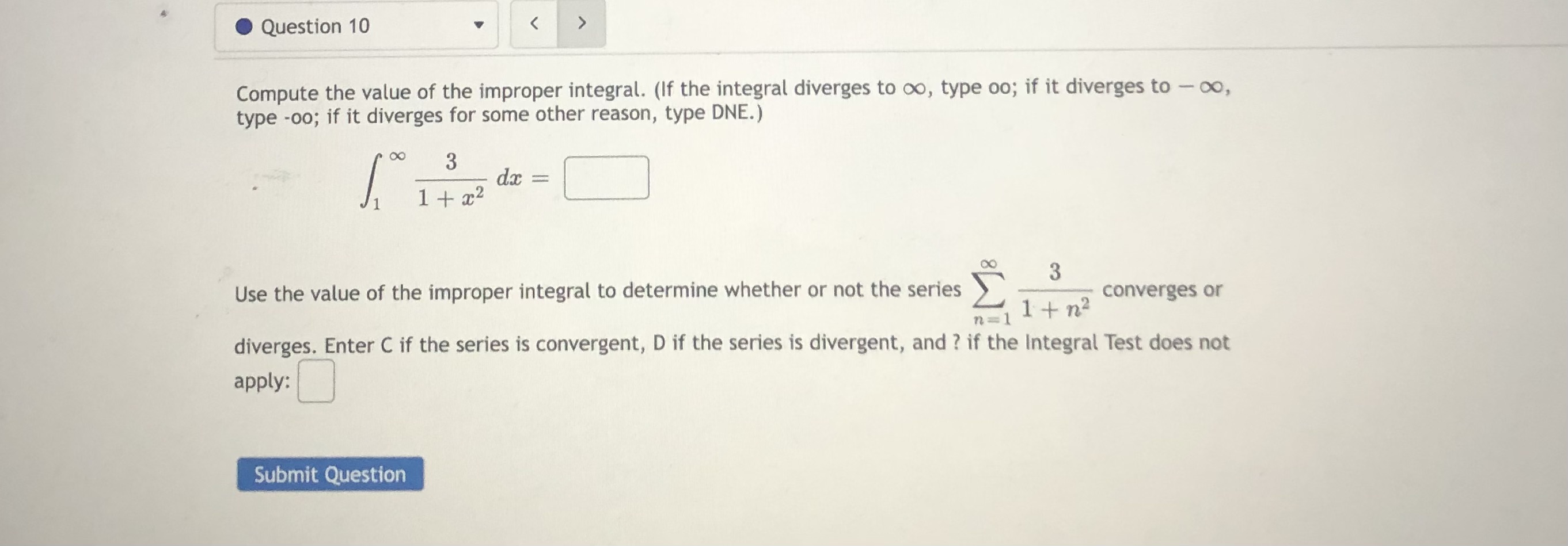
Question: please write every answer with question number please double check the answer Question 10 Compute the value of the improper integral. (If the integral diverges
please write every answer with question number
please double check the answer



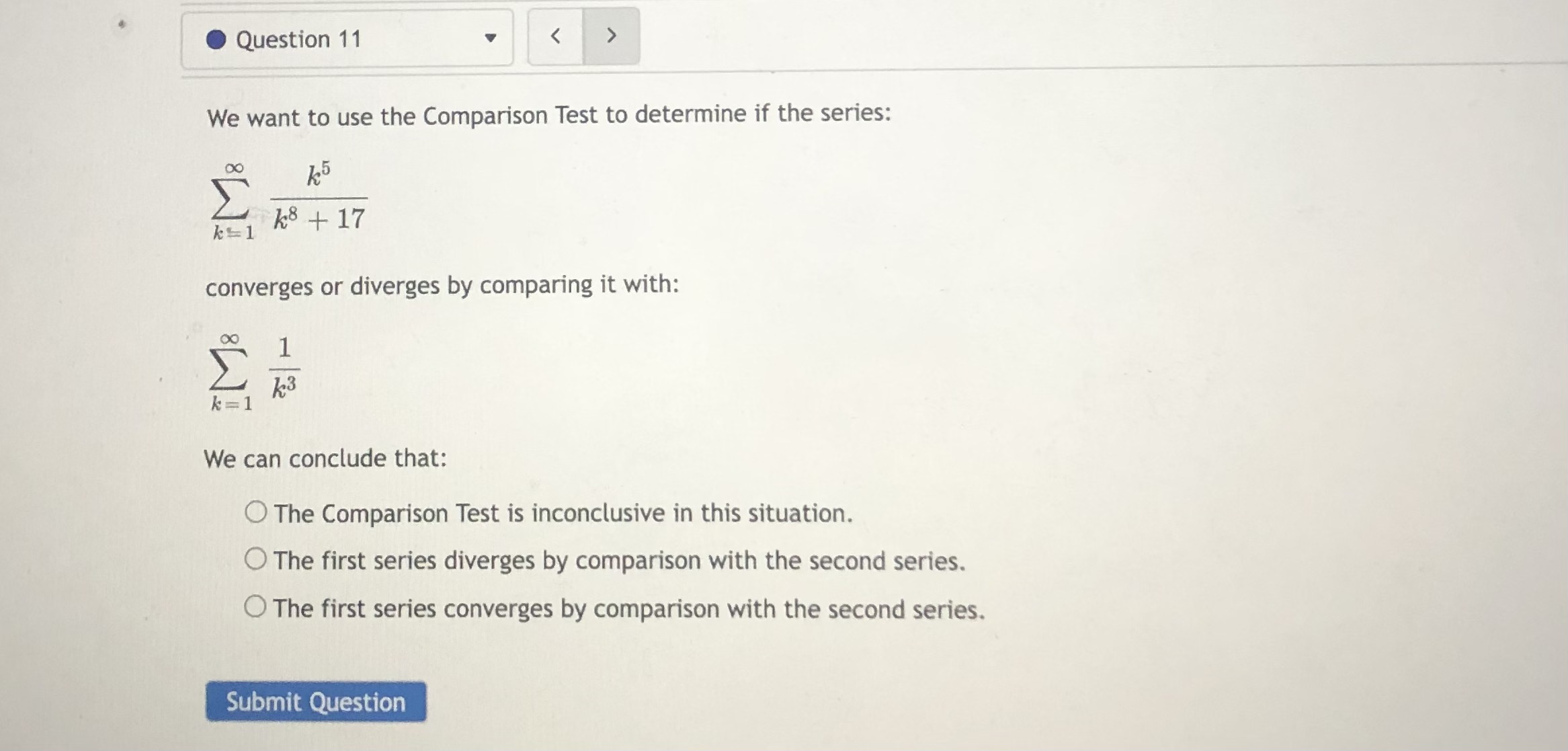
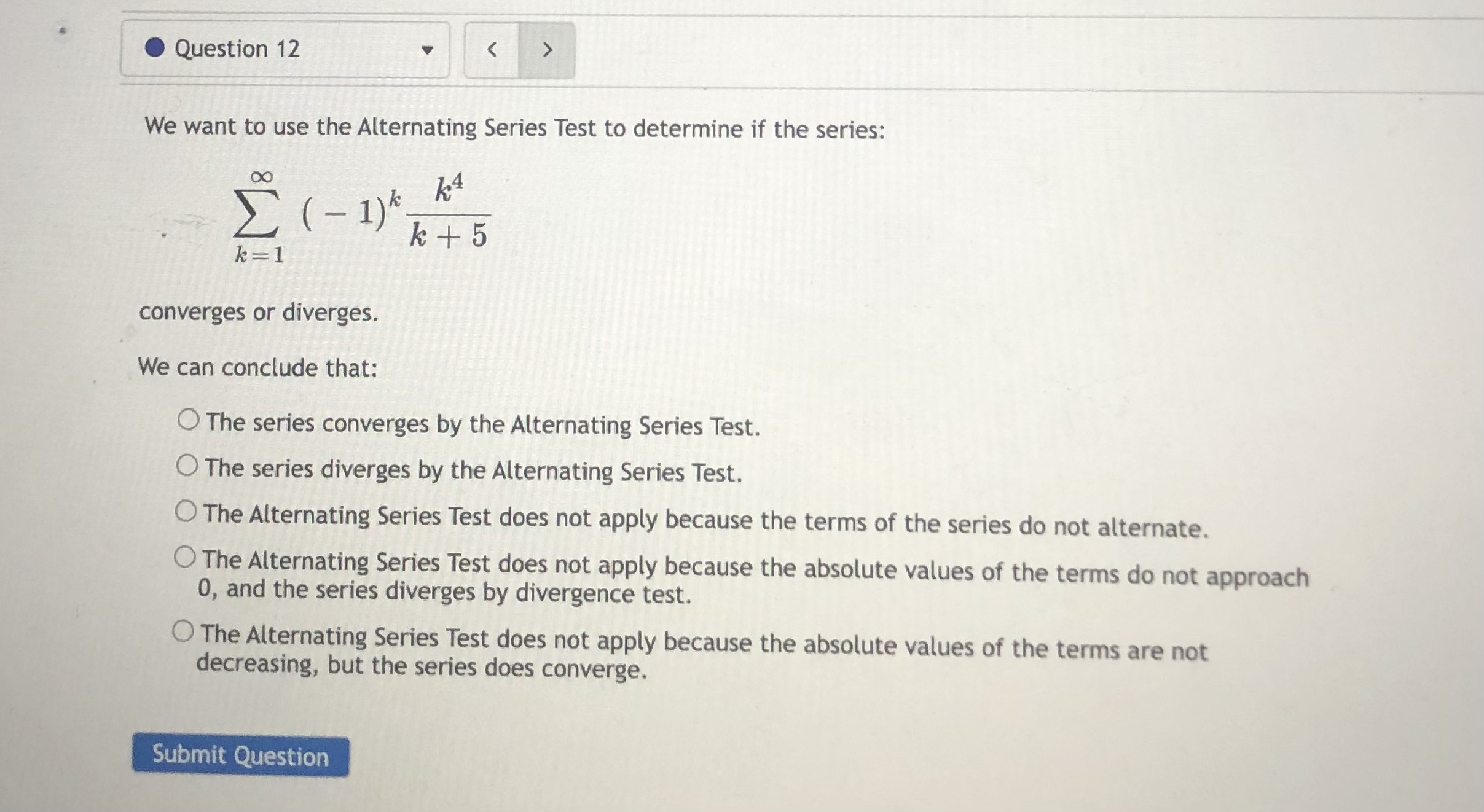
Question 10 Compute the value of the improper integral. (If the integral diverges to oo, type oo; if it diverges to - co, type -oo; if it diverges for some other reason, type DNE.) OO 3 dx = 1 + 22 3 Use the value of the improper integral to determine whether or not the series 1 + n2 converges or n=1 diverges. Enter C if the series is convergent, D if the series is divergent, and ? if the Integral Test does not apply: Submit QuestionQuestion 11 We want to use the Comparison Test to determine if the series: 15 *= 1 K8 + 17 converges or diverges by comparing it with: OO K3 k =1 We can conclude that: O The Comparison Test is inconclusive in this situation. O The first series diverges by comparison with the second series. O The first series converges by comparison with the second series. Submit QuestionQuestion 12 We want to use the Alternating Series Test to determine if the series: E ( - 1) * K 4 k + 5 k =1 converges or diverges. We can conclude that: The series converges by the Alternating Series Test. O The series diverges by the Alternating Series Test. The Alternating Series Test does not apply because the terms of the series do not alternate. O The Alternating Series Test does not apply because the absolute values of the terms do not approach 0, and the series diverges by divergence test. O The Alternating Series Test does not apply because the absolute values of the terms are not decreasing, but the series does converge. Submit
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


