please write MATLAB CODE FOR THIS

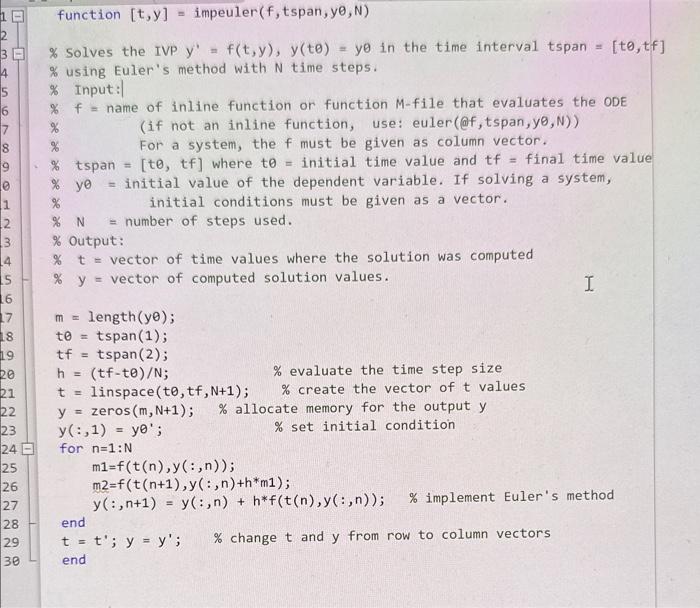
4. Consider the IVP: y=0.5y,y(0)=1;0t6 (a) Determine the Improved Euler's approximation for N=60,N=600 and N=6000. Fill in the following table with the values of the approximations, errors and ratios of consecutive errors at t=6. Two values have already been entered to help you check your results. Recall that the exact solution to the ODE is y(t)=e0.5t. Include the table in your report, as well as the MATL AB commands used to find the entries. (b) Examine the last column. How does the ratio of the errors relate to the number of steps used? Your answer to this question should confirm the fact that Improved Euler's method is a "second-order" method. That is, every time the step size is decreased by a factor k, the error is reduced (approximately) by a factor of k2. Note: Since Euler's method is only of the 1st order, the Improved Euler's method is more efficient (hence the "improved"). function [t,y]= impeuler (f,tspan,y,N) \% Solves the IVP y=f(t,y),y(t)=y in the time interval tspan =[t,tf] % using Euler's method with N time steps. \% Input:| \% f= name of inline function or function M-file that evaluates the ODE (if not an inline function, use: euler(@f,tspan, y,N) ) \% For a system, the f must be given as column vector. % yo = initial value of the dependent variable. If solving a system, \% initial conditions must be given as a vector. \% N= number of steps used. % Output: %t= vector of time values where the solution was computed %y= vector of computed solution values