Please write the program in C++.

Problem: Implement the indirect(mutually)recursive max_value and min_value functions specified in this link(https://en.wikipedia.org/wiki/Minimax), and use them to find the max (root's value) of a tree read in from the keyboard as a nested list. For example, the input tree would be: ((3,12,8),(2,4,6),(14,5,2)) 

Visual representation of the input:

( Root ) Max

/ | \

( ) ( ) ( ) Min

/ | \ / | \ / | \

3 12 8 2 4 6 14 5 2

Visual representation of the MiniMax algorithm:

( 3 ) Max

/ | \

( 3 ) ( 2 ) ( 2 ) Min

/ | \ / | \ / | \

3 12 8 2 4 6 14 5 2

And so the output should be 3, because 3 will be the max return value after the minimax tree program finished running.

So basically we prompt a message asking the user to input a tree(nested list), and the user enters the nested list specified above. To go more into detail of what can be done:

The input minimax tree could be any height or have any degree of nesting. Therefore you could either, write a recursive operator >> to read a minimax tree into a Node, or read the nested list as a string and then parse the string to build the tree. So the tree then would look with the above input like so:

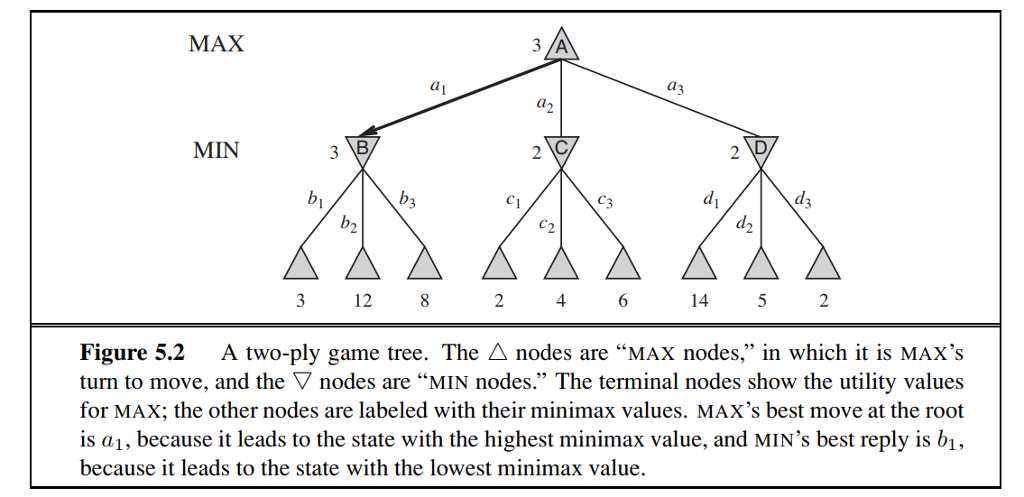
Once it goes through and evaluates the minimax tree, the output then will be 3.

If you have any questions, let me know. Thanks.

p.s. IF YOU can do the problem above in PYTHON, then if you can please add comments and proper indention.

MAX 3 A a1 3 MIN b1 di d. 3 12 8 4 14 5 2 Figure 5.2 A two-ply game tree. The nodes are "MAX nodes," in which it is MAX's turn to move, and the nodes are "MIN nodes." The terminal nodes show the utility values for MAX; the other nodes are labeled with their minimax values. MAX's best move at the root is a1, because it leads to the state with the highest minimax value, and MIN's best reply is bi, because it leads to the state with the lowest minimax value