Pls don't copy a meaningless answer from others question.

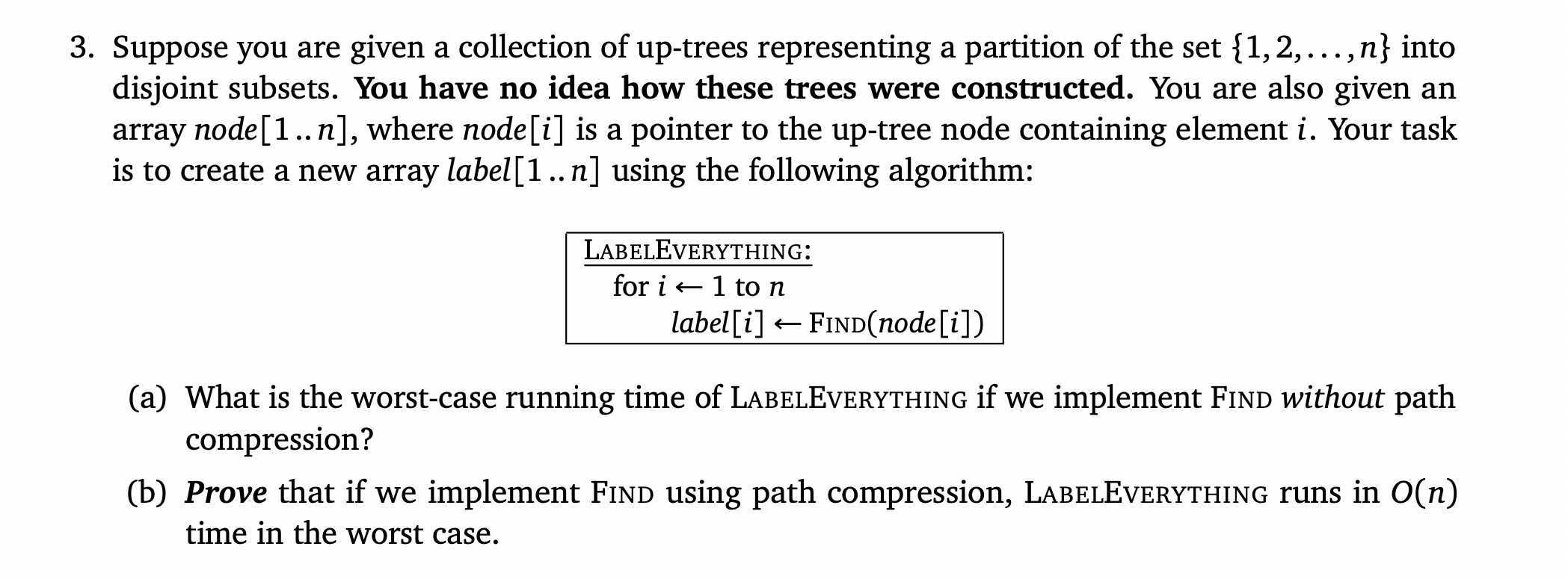
) 3. Suppose you are given a collection of up-trees representing a partition of the set {1, 2,..., n} into disjoint subsets. You have no idea how these trees were constructed. You are also given an array node[1.. n], where node[i] is a pointer to the up-tree node containing element i. Your task is to create a new array label[1 ..n] using the following algorithm: LABELEVERYTHING: for i=1 to n label[i] FIND(node[i]) (a) What is the worst-case running time of LABELEVERYTHING if we implement Find without path compression? (b) Prove that if we implement FIND using path compression, LABELEVERYTHING runs in O(n) time in the worst case