plz explain me this ans

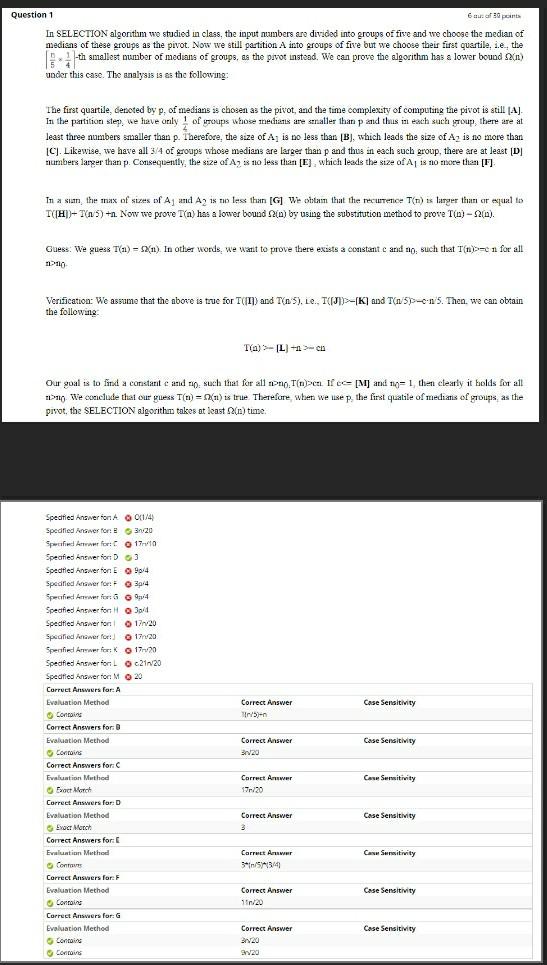
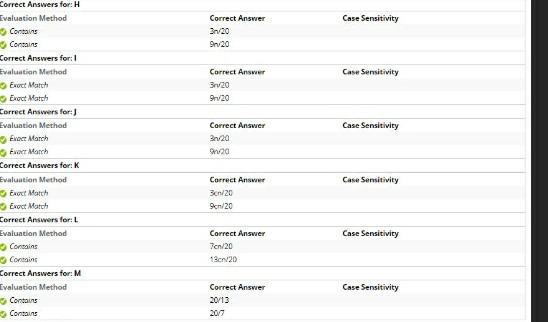
In SELECTION algorithm wo stadied in class, the input aumbers ars divided into groups of five and we choose the median of medians of these groups as the pivot. Now we still partition A into groups of five but we choose their firat quartile, i.e. the [5D41]-th mallest number of medians of groups, as the pivot instead. We can prowe the algorithm has a lower bouad (n) ) under this case. The analysas is as the following: The first quartile, dencted by p, of medians is chosen as the pivot, and the time complexity of computing the pivot is still [A]. In the partition step. we have only 41 of groups whose medrims are smatler than p and thus in each such group, there are at least three numbers squalles than p. Therefore, the size of A1 is no less than [B], which leads the size of A2 is no more than [C]. Likewise, we have all 3/4 of groups whose medians are larger than p and thus in each such group, there are at least [D] numbers lareer than p. Conseguently, the size of A2 s no less than [E], which leads the size of A1 is no noce than [F]. In a sam, the max of siges of A1 and A2 is no less than [G] We oblam that the recurence T(n) is larger thatr or equal to T([H))+T(5)+n. Now we prove T(n) has a lower bound (n) by using the substitution method to pwove T(n)(n). Guess: We guess T(n)=(n). In other words, we watit to prove there exists a constant c ard no: such that I(n)=0,n for all neno. the following: T(n)>[L]+n>=n Our goal is to find a constanit c and no: such that for all nono: T(n)>ca. If cc- [M] and no; =1, then clearly it holds for all nent. We conclude that our guess T(n)=(n) is true. Therefore, when we use p, the first quatile of medians of groups, as the pirot, the SELECTION algorithm takes at least (n) tume. Correct Answers for: H Ivaluation Method Correct Answer Case Sensitivity Consains 3n/20 Conoains 9n 20 Correct Answers for: 1 Evaluatian Medhod Correct Answer Casu Sensitivity Enoc: Mathh 3nve0 Enoct Match 9rv20 Correct Answers for: J Evaluation Method Correct Answer Case Sensithity Evere March 3ne0 Fuoct Mamh snet Correct Answers for: K Evaluation Method Carrect Answar Case Sensitivity Exect Match 3criad Evect Match 9sri20 Forrect Answers for: 1 Evaluabion Method Correct Answer Case Sensithicy Concains 7enial Conerins sienv2D Correct Answers for: M Evaluation Method Correct Answier Case Sensitivity Gontains 2013 Consais 207 In SELECTION algorithm wo stadied in class, the input aumbers ars divided into groups of five and we choose the median of medians of these groups as the pivot. Now we still partition A into groups of five but we choose their firat quartile, i.e. the [5D41]-th mallest number of medians of groups, as the pivot instead. We can prowe the algorithm has a lower bouad (n) ) under this case. The analysas is as the following: The first quartile, dencted by p, of medians is chosen as the pivot, and the time complexity of computing the pivot is still [A]. In the partition step. we have only 41 of groups whose medrims are smatler than p and thus in each such group, there are at least three numbers squalles than p. Therefore, the size of A1 is no less than [B], which leads the size of A2 is no more than [C]. Likewise, we have all 3/4 of groups whose medians are larger than p and thus in each such group, there are at least [D] numbers lareer than p. Conseguently, the size of A2 s no less than [E], which leads the size of A1 is no noce than [F]. In a sam, the max of siges of A1 and A2 is no less than [G] We oblam that the recurence T(n) is larger thatr or equal to T([H))+T(5)+n. Now we prove T(n) has a lower bound (n) by using the substitution method to pwove T(n)(n). Guess: We guess T(n)=(n). In other words, we watit to prove there exists a constant c ard no: such that I(n)=0,n for all neno. the following: T(n)>[L]+n>=n Our goal is to find a constanit c and no: such that for all nono: T(n)>ca. If cc- [M] and no; =1, then clearly it holds for all nent. We conclude that our guess T(n)=(n) is true. Therefore, when we use p, the first quatile of medians of groups, as the pirot, the SELECTION algorithm takes at least (n) tume. Correct Answers for: H Ivaluation Method Correct Answer Case Sensitivity Consains 3n/20 Conoains 9n 20 Correct Answers for: 1 Evaluatian Medhod Correct Answer Casu Sensitivity Enoc: Mathh 3nve0 Enoct Match 9rv20 Correct Answers for: J Evaluation Method Correct Answer Case Sensithity Evere March 3ne0 Fuoct Mamh snet Correct Answers for: K Evaluation Method Carrect Answar Case Sensitivity Exect Match 3criad Evect Match 9sri20 Forrect Answers for: 1 Evaluabion Method Correct Answer Case Sensithicy Concains 7enial Conerins sienv2D Correct Answers for: M Evaluation Method Correct Answier Case Sensitivity Gontains 2013 Consais 207