plz provide answer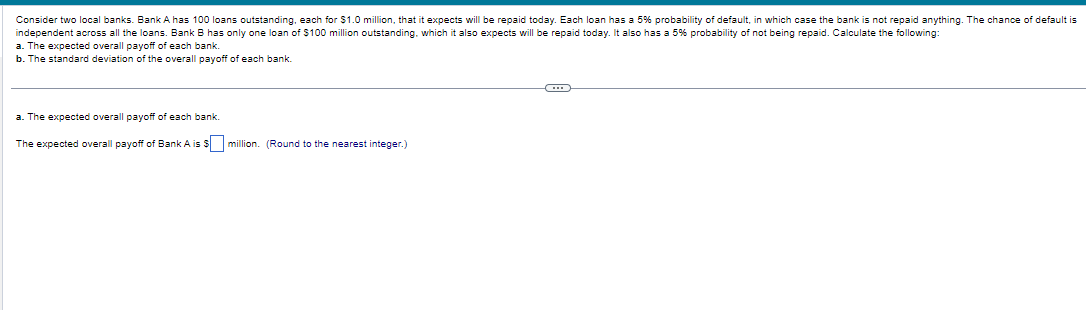

solved example is

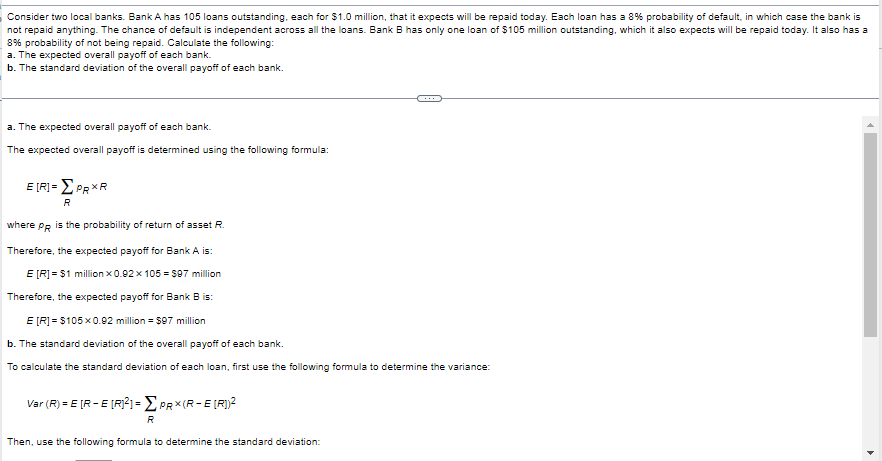
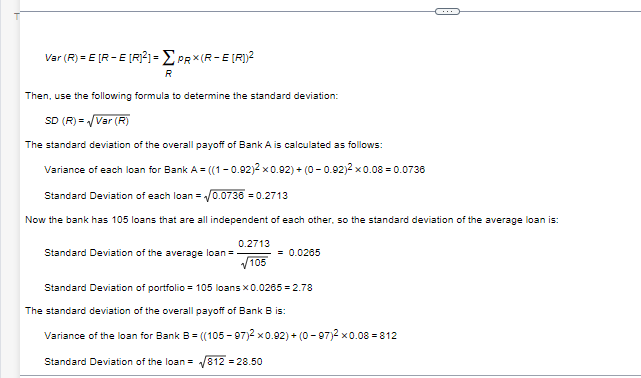
a. The expected overall payoff of each bank. b. The standard deviation of the overall payoff of each bank. a. The expected overall payoff of each bank. The expected overall payoff of Bank A is S million. (Round to the nearest integer.) Consider two local banks. Bank A has 105 loans outstanding, each for $1.0 million, that it expects will be repaid today. Each loan has a 8% probability of default, in which case the bank is not repaid anything. The chance of default is independent across all the loans. Bank B has only one loan of $105 million outstanding, which it also expects will be repaid today. It also has a 8% probability of not being repaid. Calculate the following: a. The expected overall payoff of each bank. b. The standard deviation of the overall payoff of each bank. a. The expected overall payoff of each bank. The expected overall payoff is determined using the following formula: E[R]=RpRR where pR is the probability of return of asset R. Therefore, the expected payoff for Bank A is: E[R]=$1million0.92105=$97million Therefore, the expected payoff for Bank B is: E[R]=$1050.92million=$97million b. The standard deviation of the overall payoff of each bank. To calculate the standard deviation of each loan, first use the following formula to determine the variance: Var(R)=E[RE[R]2]=RpR(RE[R])2 Then, use the following formula to determine the standard deviation: Var(R)=E[RE[R]2]=RpR(RE[R])2 Then, use the following formula to determine the standard deviation: SD(R)=Var(R) The standard deviation of the overall payoff of Bank A is calculated as follows: Variance of each loan for Bank A=((10.92)20.92)+(00.92)20.08=0.0736 Standard Deviation of each loan =0.0736=0.2713 Now the bank has 105 loans that are all independent of each other, so the standard deviation of the average loan is: Standard Deviation of the average loan =1050.2713=0.0265 Standard Deviation of portfolio =105 loans 0.0265=2.78 The standard deviation of the overall payoff of Bank B is: Variance of the loan for Bank B=((10597)20.92)+(097)20.08=812 Standard Deviation of the loan =812=28.50