plz write clearly
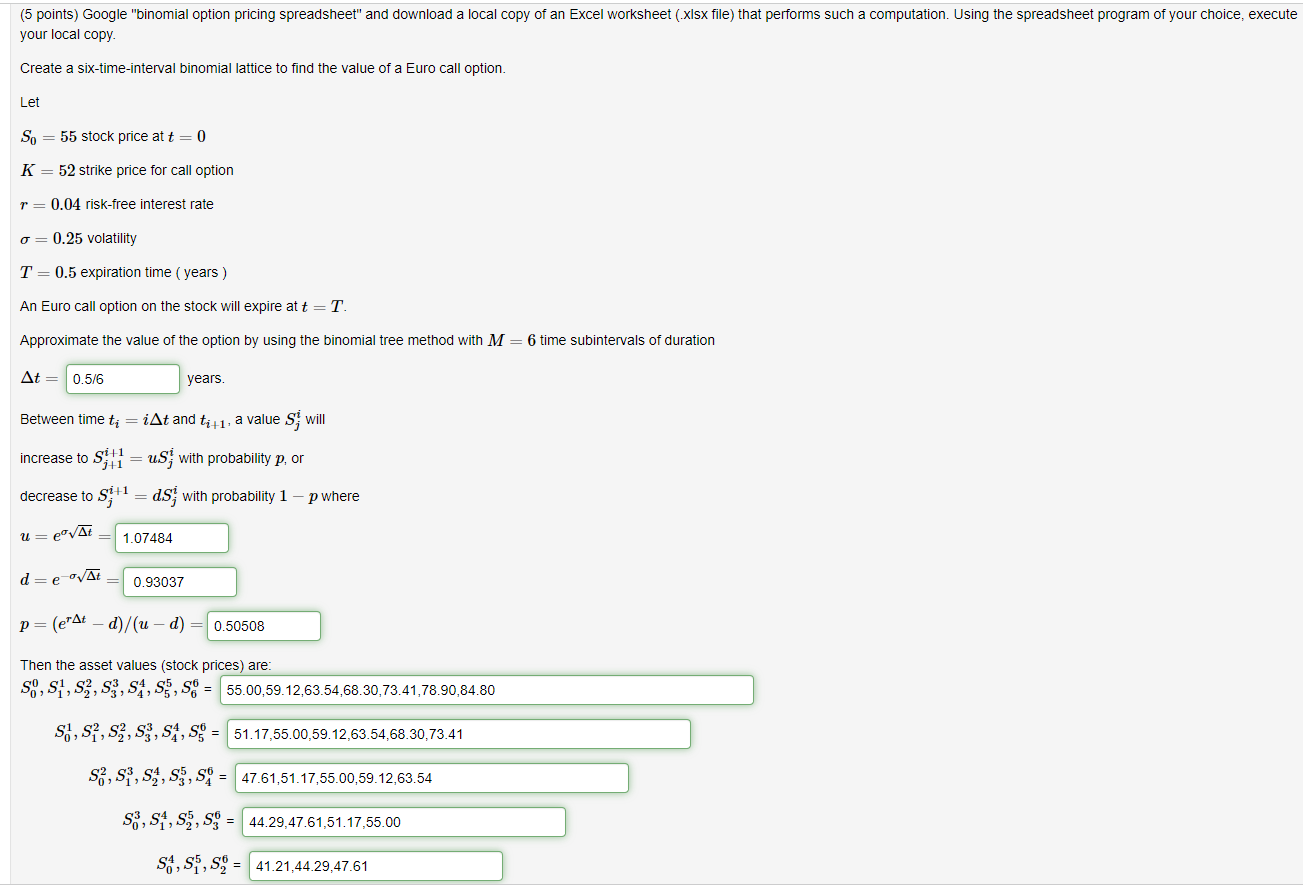
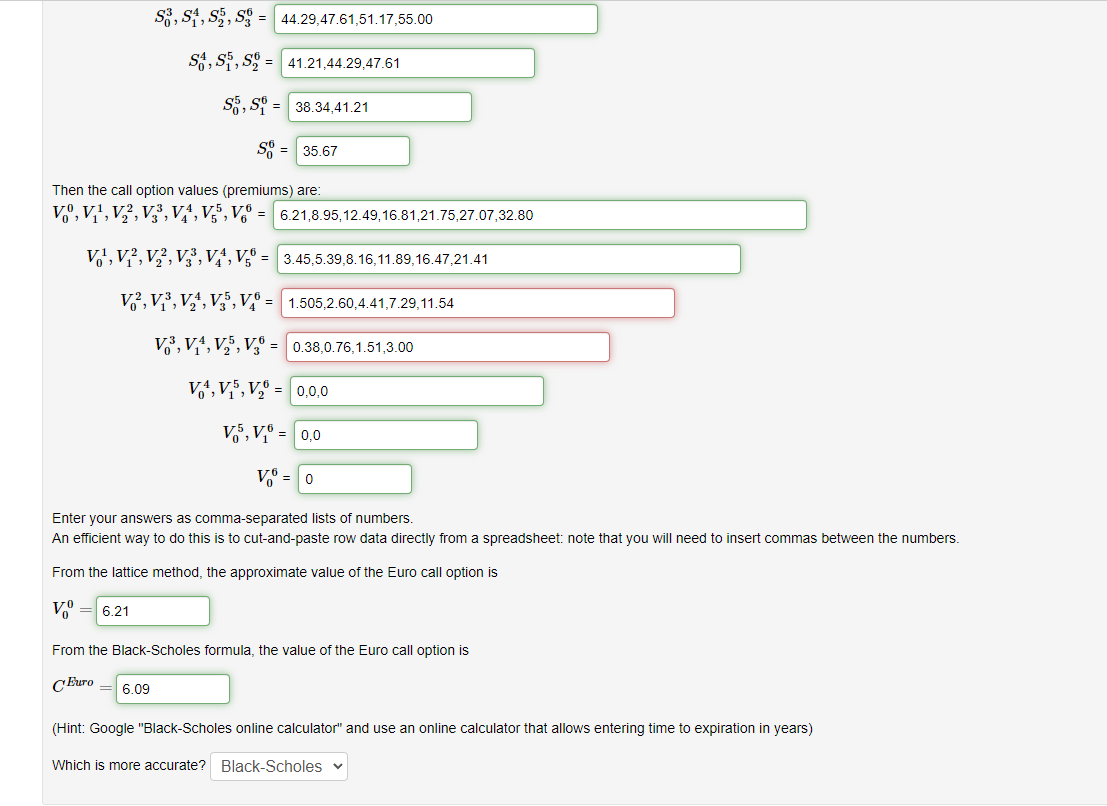
(5 points) Google "binomial option pricing spreadsheet" and download a local copy of an Excel worksheet (.xlsx file) that performs such a computation. Using the spreadsheet program of your choice, execute your local copy Create a six-time-interval binomial lattice to find the value of a Euro call option. Let So = 55 stock price at t = 0 K = 52 strike price for call option r=0.04 risk-free interest rate o= 0.25 volatility T=0.5 expiration time (years) An Euro call option on the stock will expire at t =T. Approximate the value of the option by using the binomial tree method with M = 6 time subintervals of duration At= 0.5/6 years. Between time t= iAt and ti+1, a value S will increase to S11 = us with probability p, or SI = ds with probability 1 - p where decrease to u= e At 1.07484 d=e-At 0.93037 p= (erat d)/(u - d) = 0.50508 Then the asset values (stock prices) are: S0, S1, S2, S3, S4, S5, S. = 55.00,59.12,63.54,68.30,73.41,78.90,84.80 Sy, S, S2, S3, S4, S5 = 51.17,55.00,59.12,63.54,68.30,73.41 S2, S, S, s, so = 47.61,51.17,55.00,59.12,63.54 S3, S1, s, so = 44.29,47.61,51.17,55.00 SA, S, = 41.21,44.29,47.61 S3, S4, S, S= 44.29,47.61,51.17,55.00 SA, S, S9 = 41.21,44.29,47.61 S, S = 38.34,41.21 SO = 35.67 Then the call option values (premiums) are: V.",V,',V,V,V,4, 155, V. = 6.21,8.95,12.49,16.81,21.75,27.07,32.80 V,',V,?, V,,V3, V., V. = 3.45,5.39,8.16,11.89,16.47,21.41 = V,?, V3, V,4, V5, VA 1.505,2.60,4.41,7.29,11.54 V.3, V,4,V,,V= 0.38,0.76,1.51,3.00 V, V, V = 0.0.0 V5, V = 0,0 V = 0 Enter your answers as comma-separated lists of numbers. An efficient way to do this is to cut-and-paste row data directly from a spreadsheet: note that you will need to insert commas between the numbers. From the lattice method, the approximate value of the Euro call option is V = 6.21 From the Black-Scholes formula, the value of the Euro call option is Euro 6.09 (Hint: Google "Black-Scholes online calculator" and use an online calculator that allows entering time to expiration in years) Which is more accurate? Black-Scholes (5 points) Google "binomial option pricing spreadsheet" and download a local copy of an Excel worksheet (.xlsx file) that performs such a computation. Using the spreadsheet program of your choice, execute your local copy Create a six-time-interval binomial lattice to find the value of a Euro call option. Let So = 55 stock price at t = 0 K = 52 strike price for call option r=0.04 risk-free interest rate o= 0.25 volatility T=0.5 expiration time (years) An Euro call option on the stock will expire at t =T. Approximate the value of the option by using the binomial tree method with M = 6 time subintervals of duration At= 0.5/6 years. Between time t= iAt and ti+1, a value S will increase to S11 = us with probability p, or SI = ds with probability 1 - p where decrease to u= e At 1.07484 d=e-At 0.93037 p= (erat d)/(u - d) = 0.50508 Then the asset values (stock prices) are: S0, S1, S2, S3, S4, S5, S. = 55.00,59.12,63.54,68.30,73.41,78.90,84.80 Sy, S, S2, S3, S4, S5 = 51.17,55.00,59.12,63.54,68.30,73.41 S2, S, S, s, so = 47.61,51.17,55.00,59.12,63.54 S3, S1, s, so = 44.29,47.61,51.17,55.00 SA, S, = 41.21,44.29,47.61 S3, S4, S, S= 44.29,47.61,51.17,55.00 SA, S, S9 = 41.21,44.29,47.61 S, S = 38.34,41.21 SO = 35.67 Then the call option values (premiums) are: V.",V,',V,V,V,4, 155, V. = 6.21,8.95,12.49,16.81,21.75,27.07,32.80 V,',V,?, V,,V3, V., V. = 3.45,5.39,8.16,11.89,16.47,21.41 = V,?, V3, V,4, V5, VA 1.505,2.60,4.41,7.29,11.54 V.3, V,4,V,,V= 0.38,0.76,1.51,3.00 V, V, V = 0.0.0 V5, V = 0,0 V = 0 Enter your answers as comma-separated lists of numbers. An efficient way to do this is to cut-and-paste row data directly from a spreadsheet: note that you will need to insert commas between the numbers. From the lattice method, the approximate value of the Euro call option is V = 6.21 From the Black-Scholes formula, the value of the Euro call option is Euro 6.09 (Hint: Google "Black-Scholes online calculator" and use an online calculator that allows entering time to expiration in years) Which is more accurate? Black-Scholes
