PM Mon Jun $30$

SCAICET$9$

$4\mathrm{.}2\mathrm{.}030.$MI$.$SA$.$

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part.

Tutorial Exercise

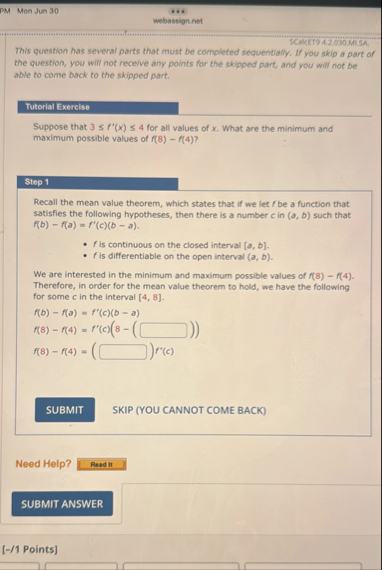
Suppose that $3f^{\text{'}}(x)4$ for all values of $x.$ What are the minimum and maximum possible values of $f(8)-f(4)?$

Step $1$

Recall the mean value theorem, which states that if we let $f$ be a function that satisfies the following hypotheses, then there is a number $c$ in $(a,b)$ such that $f(b)-f(a)=f^{\text{'}}(c)(b-a).$

$f$ is continuous on the closed interval $a,b.$

$f$ is differentiable on the open interval $(a,b).$

We are interested in the minimum and maximum possible values of $f(8)-f(4).$ Therefore, in order for the mean value theorem to hold, we have the following for some $c$ in the interval $4,8.$

$f(b)-f(a)=f^{\text{'}}(c)(b-a)$

$f(8)-f(4)=f^{\text{'}}(c)(8-())$

$f(8)-f(4)=()f^{\text{'}}(c)$

Need Help? $$

$[-/1$ Points$]$