Question: polynomial_main.c: #include #include #include #include polynomial.h void display_polynomial(float p[], int n, float x) { int i; for (i=0; i EPSILON && i !=0) printf(+); printf(%.2f*%.2f^%d,
![polynomial_main.c: #include #include #include #include "polynomial.h" void display_polynomial(float p[], int n,](https://s3.amazonaws.com/si.experts.images/answers/2024/09/66e1d0b6b8cbc_06266e1d0b632ebf.jpg)
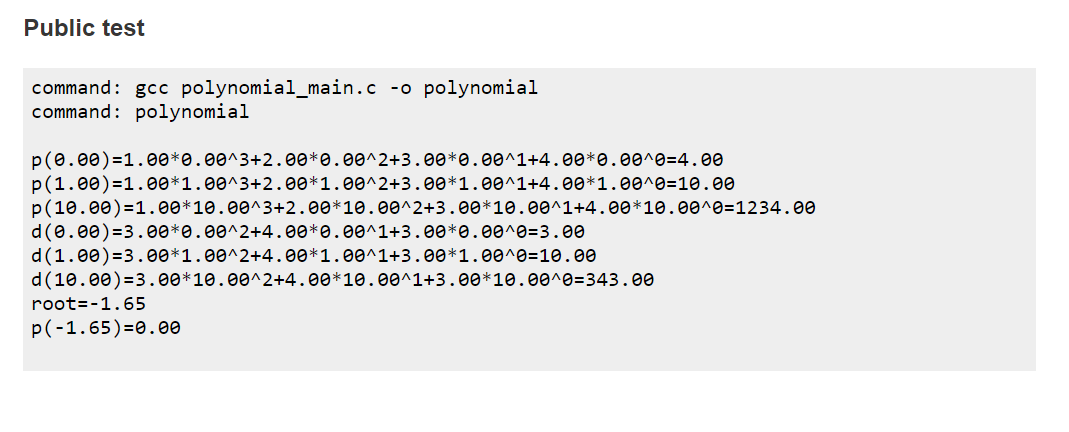
polynomial_main.c: #include
void display_polynomial(float p[], int n, float x) { int i; for (i=0; i return 0; } polynomial.h:/* * your program signature */ #ifndef POLYNOMIAL_H #define POLYNOMIAL_H #include
Write a C program, polynomial.h, containing the following polynomial operation functions: 1. float horner(float p[], int n, float x ), which computes and returns the value of the following (n1)-th degree polynomial p(x) of coefficients p[0],,p[n 1]. p(x)=p[0]xn1+p[1]xn2++p[n2]x1+p[n1]x0 It is required to use Horner's algorithm (supplementary link). 2. void derivative(float p[], int n, float d[], which computes the derivative of input (n-1)-th degree polynomial by p[], output the derivative of (n2)-th degree polynomial to array d[]. The derivative of the above polynomial p(x) is as follows. p(x)=(n1)p[0]xn2+(n2)p[1]xn3++p[n2]x0 3. float newton(float p[], int n, float x ), which finds an approximate real root x of polynomial p(x) using the Newton's method with start position x. Use the fault tolerant 1e6 (or 0.000001 ) as a stop condition, i.e., if r is the actual root, stop the iteration if xr
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


