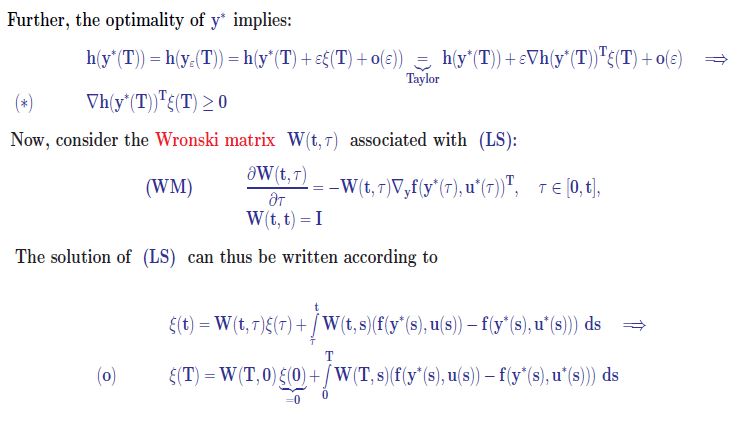(Pontrjagin's Minimum Principle, Part II). Optimization course , Related Notes are attached!

This is about (Pontriagin's Minimum Principle, Part II). I am attaching the notes! Let A, B E R"x" be n x n matrices, G, Q e 1Rox" symmetric positive definite n x n matrices, yo ( R", n E N, Umin, Umar E IR with umin 0. Consider the optimal control problem T T maximize J(y, u) := y(T) Gy(T) + y(t) Qy(t) at + r u(t)2 dt, subject to y(t) = Ay(t) + u(t) By(t) , te [0, T], y(0) = yo : u(t) EU(u(t)) := [umin, Umar], te [0, T] . Consider the operator K(u(t)) := max(Umin, min( Umax, -= p*(t) By* (t))), and show that there exists a constant C' > 0 such that, if C'|| Billly.| |T p*(to) fly*(to), u( to)) It follows that there exists an interval I(to) C 0, T), such that p (t ) fly (t ), u' (t) > p'(t) fly (t), u(t), te I(to). We define u(t) , tel(to) u(t) = Fu*(t) , to I(to) Observing p*(t) = W(T, t)"p*(T), this is a contradiction to (x).Let us now consider the general case: T J(y, u) = h(y(T)) + /gly(t), u(t)). It can be reformulated as the terminal cost problem: J(y, u) = h(y(T)) + y(T) by introducing the additional differential equation y(t) = g(y(t), u(t)), te [0, T]. Homework: Use similar arguments as before to conclude