Populations that can be modeled by the modified logistic equation

$\frac{dP}{dt}=P(bP-a)$

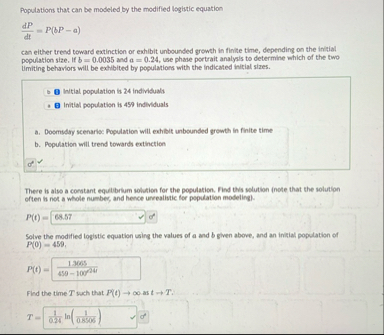
can either trend toward extinction or exhibit unbounded growth in finite time, depending on the initial population size. If $b=0\mathrm{.}0035$ and $a=0\mathrm{.}24,$ use phase portrait analysis to determine which of the two limiting behaviors will be exibited by populations with the indicated initial sizes.

b $0$ initial population is $24$ individuals

B Initial population is $459$ individuals

a$.$ Doomiday scenarisc Population will exhibit unbounded growth in finite time

b$.$ Population will trend towards extinction

$a^2$

There is also a constant equilibrium solution for the population. Find this solution $($note that the solution often is not a whole number, and hence urrealistic for popdation modeling$).$

$P(t)=$

Solve the modified logistic equation using the values of a and $b$ given above, and an initial population of $P(0)=459.$

$P(t)=$

Find the time $T$ such that $P(t)$ as $tT.$