Practical work

$2023-2024$

The practical work of the OR course consists of writing a Julia program using the JuMP library to solve an optimization problem. The problem and its variant is an application of the shortest path problem.

Problems definition and examples

Given $G=(V,E)$ a directed graph with $V=\{v_1,$cdots,$v_n\}$ the set of the vertices of $G,E$ the set of the arcs of $G$ and a positive distance $d_{ij}$ associated with each arc $(i,j)$ of $E,$ the problem consists in finding a shortest path from $v_1$ to $v_n($if it exists$).$ The distance of the path is the sum of all the distances of the arcs of the path. This problem will be denoted $P_1$ in the following.

A variant of problem $P_1,$ denoted $P_2$ will consist in finding two arc$-$disjoint paths such that the sum of their respective length is minimal. Both paths start from $v_1$ and end in $v_n.$ Two paths are said to be arc$-$disjoint if they have no arc in common.

We consider the following weighted directed graph $G_1$ :

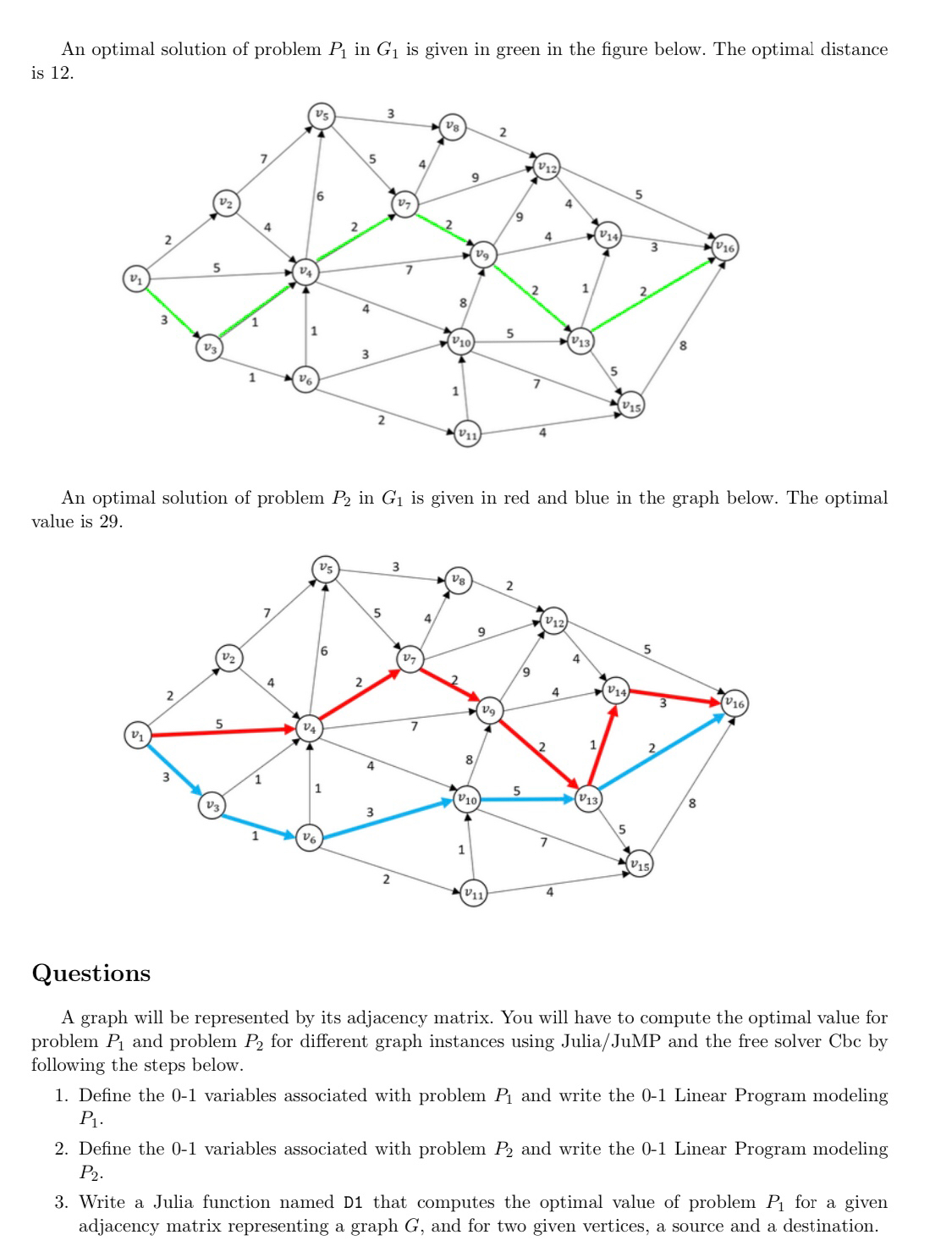
An optimal solution of problem $P_1$ in $G_1$ is given in green in the figure below. The optimal distance is $12.$

An optimal solution of problem $P_2$ in $G_1$ is given in red and blue in the graph below. The optimal value is $29.$

Questions

A graph will be represented by its adjacency matrix. You will have to compute the optimal value for problem $P_1$ and problem $P_2$ for different graph instances using Julia$/$JuMP and the free solver Cbc by following the steps below.

Define the $0-1$ variables associated with problem $P_1$ and write the $0-1$ Linear Program modeling $P_1.$

Define the $0-1$ variables associated with problem $P_2$ and write the $0-1$ Linear Program modeling $P_2.$

Write a Julia function named D$1$ that computes the optimal value of problem $P_1$ for a given adjacency matrix representing a graph $G,$ and for two given vertices, a source and a destination.