Practice problem $2$:

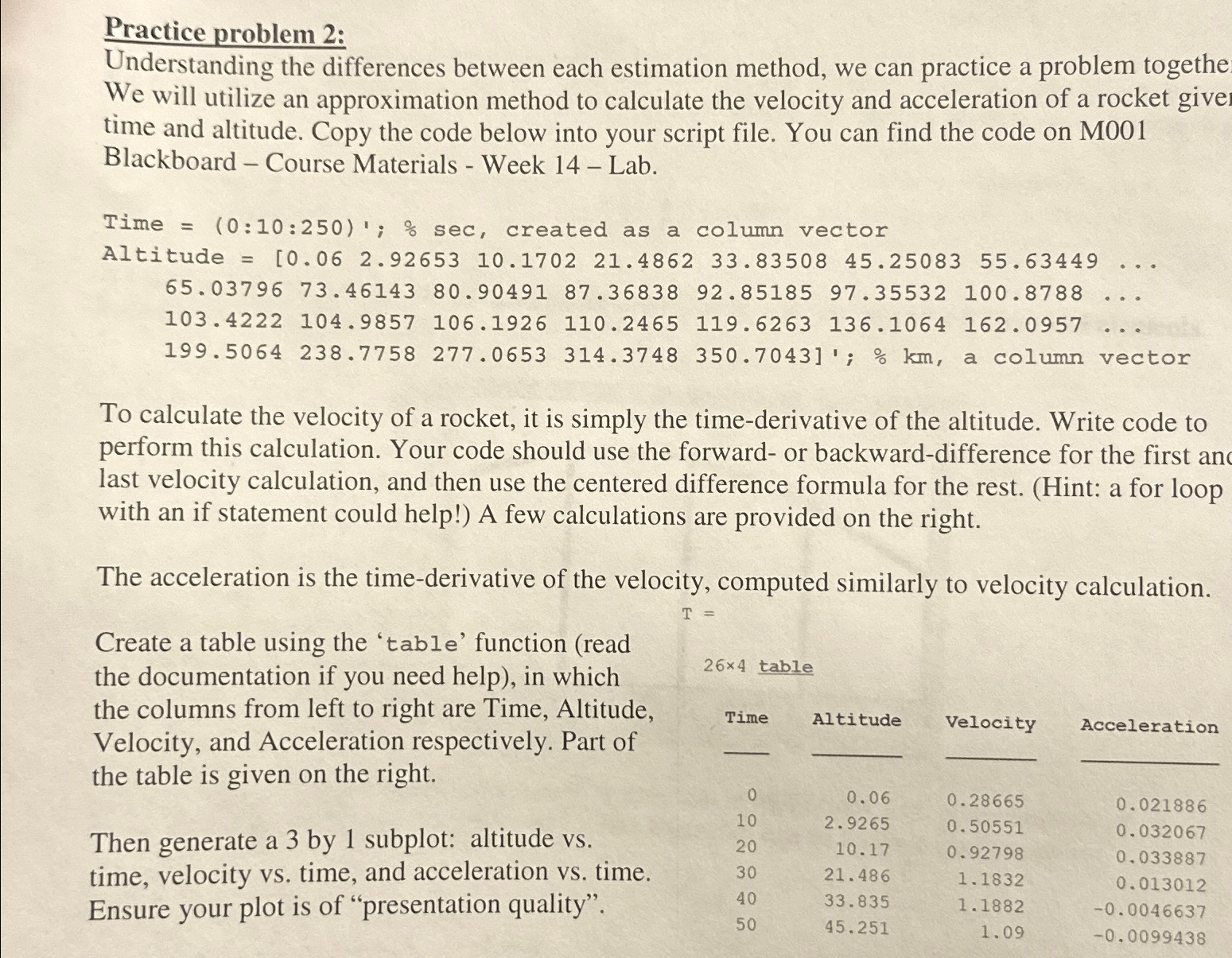
Understanding the differences between each estimation method, we can practice a problem togethe We will utilize an approximation method to calculate the velocity and acceleration of a rocket give time and altitude. Copy the code below into your script file. You can find the code on M$001$ Blackboard $-$ Course Materials $-$ Week $14-$ Lab.To calculate the velocity of a rocket, it is simply the time$-$derivative of the altitude. Write code to perform this calculation. Your code should use the forward$-$ or backward$-$difference for the first an last velocity calculation, and then use the centered difference formula for the rest. $($Hint: a for loop with an if statement could help!$)$ A few calculations are provided on the right.

The acceleration is the time$-$derivative of the velocity, computed similarly to velocity calculation.

Create a table using the $\text{'}$ table $\text{'}$ function $($read the documentation if you need help$),$ in which the columns from left to right are Time, Altitude, Velocity, and Acceleration respectively. Part of the table is given on the right.

Then generate a $3$ by $1$ subplot: altitude vs$.$ time, velocity vs$.$ time, and acceleration vs$.$ time. Ensure your plot is of "presentation quality".

$T=$

$264$ table

$\backslash$table$[[$Time$,$Altitude,Velocity,Acceleration$],[0,0\mathrm{.}06,0\mathrm{.}28665,0\mathrm{.}021886],[10,2\mathrm{.}9265,0\mathrm{.}50551,0\mathrm{.}032067],[20,10\mathrm{.}17,0\mathrm{.}92798,0\mathrm{.}033887],[30,21\mathrm{.}486,1\mathrm{.}1832,0\mathrm{.}013012],[40,33\mathrm{.}835,1\mathrm{.}1882,-0\mathrm{.}0046637],[50,45\mathrm{.}251,1\mathrm{.}09,-0\mathrm{.}0099438]]$