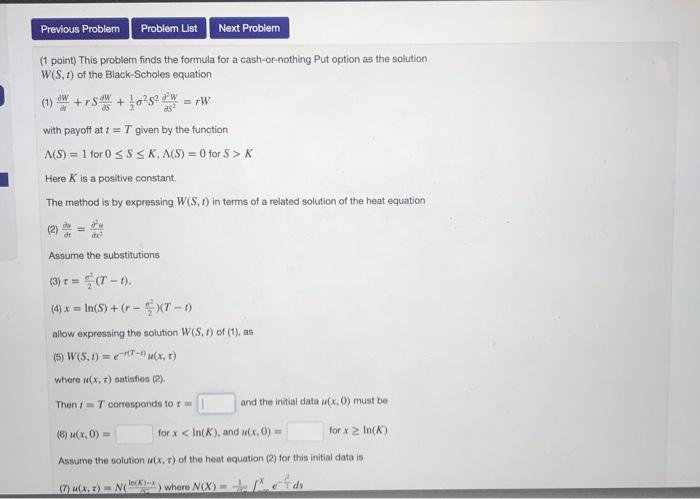
Question: Previous Problem Problem List Next Problem =rW (1 point) This problem finds the formula for a cash-or-nothing Put option as the solution W(S. 1) of
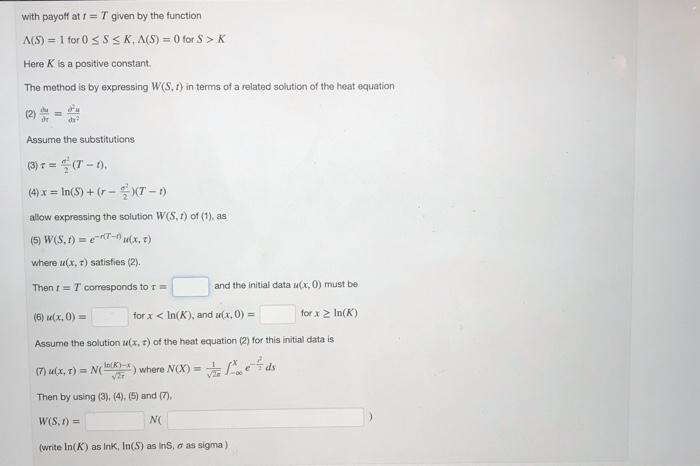
Previous Problem Problem List Next Problem =rW (1 point) This problem finds the formula for a cash-or-nothing Put option as the solution W(S. 1) of the Black-Scholes equation (1)*+rs + mo? 52. W with payoff at 1 = T given by the function A(S) = 1 for 0 SS SK,A(S) = 0 for S > K Here K is a positive constant The method is by expressing W(S. ) in terms of a related solution of the heat equation (2) Assume the substitutions (3) +(T-1). (4) x = In()+(r - (T-1) allow expressing the solution W(S. 1) of (1), as (5) W(S. 1) = -(x, ) where x T) satisfies (2) Then corresponds to and the initial data (x,0) must be (6) UC,0) for x K Here K is a positive constant The method is by expressing W(S. 1) in terms of a related solution of the heat equation Assume the substitutions (3) + = (T-1). In(S)+(-XT- allow expressing the solution W(S. 1) of (1), as (5) W(S. 1) = n(X. ) where (x, t) satisfies (2). Then I = T corresponds to = and the initial data (x,0) must be (6) (x,0) = for x In(K) Assume the solution u(x, t) of the heat equation (2) for this initial data is (7) M(x, 1) = n(hock) where N(X) = leds Then by using (3), (4), (5) and (7) W(S. 1) = NO (write In(K) as Ink, In(S) as ins, das sigma) Previous Problem Problem List Next Problem =rW (1 point) This problem finds the formula for a cash-or-nothing Put option as the solution W(S. 1) of the Black-Scholes equation (1)*+rs + mo? 52. W with payoff at 1 = T given by the function A(S) = 1 for 0 SS SK,A(S) = 0 for S > K Here K is a positive constant The method is by expressing W(S. ) in terms of a related solution of the heat equation (2) Assume the substitutions (3) +(T-1). (4) x = In()+(r - (T-1) allow expressing the solution W(S. 1) of (1), as (5) W(S. 1) = -(x, ) where x T) satisfies (2) Then corresponds to and the initial data (x,0) must be (6) UC,0) for x K Here K is a positive constant The method is by expressing W(S. 1) in terms of a related solution of the heat equation Assume the substitutions (3) + = (T-1). In(S)+(-XT- allow expressing the solution W(S. 1) of (1), as (5) W(S. 1) = n(X. ) where (x, t) satisfies (2). Then I = T corresponds to = and the initial data (x,0) must be (6) (x,0) = for x In(K) Assume the solution u(x, t) of the heat equation (2) for this initial data is (7) M(x, 1) = n(hock) where N(X) = leds Then by using (3), (4), (5) and (7) W(S. 1) = NO (write In(K) as Ink, In(S) as ins, das sigma)