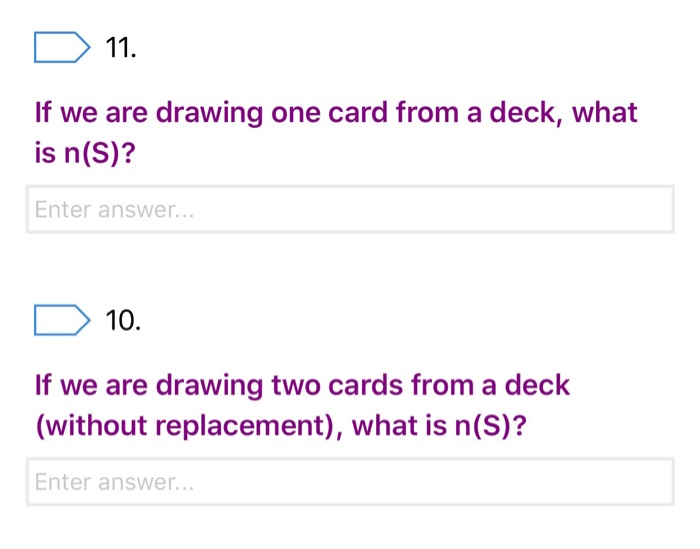
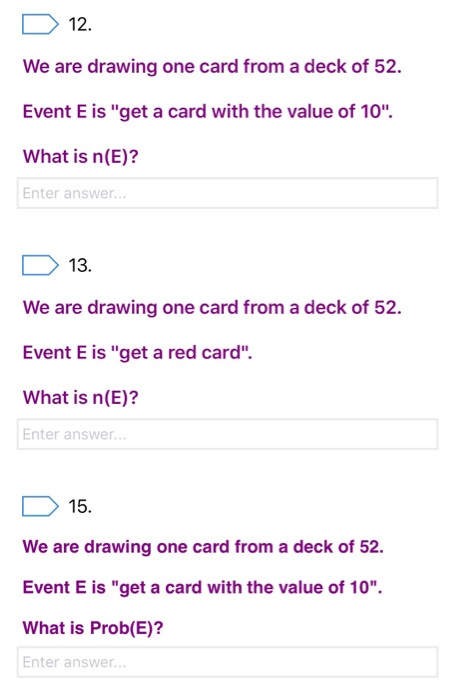
Previously, in combinatorics, we figured out how many possible outcomes there would be given some criteria. In Probability, we will use this "amount of outcomes" to help us calculate probability of some event occurring. Terms: . The sample space is the set S of al possible outcomes. e.g., if we're flipping a coin twice, the outcomes would be More often, we want the size of the sample space S. This is written as n(S). For flipping a coin twice, the size of the sample space is n(S) 4 . . When doing an experiment, we have some event E we are checking for. E is also a set. e.g., if we're flipping a coin twice and want to see how many outcomes have exactly one Head, the event space would be: {(H, T), (T, H) }