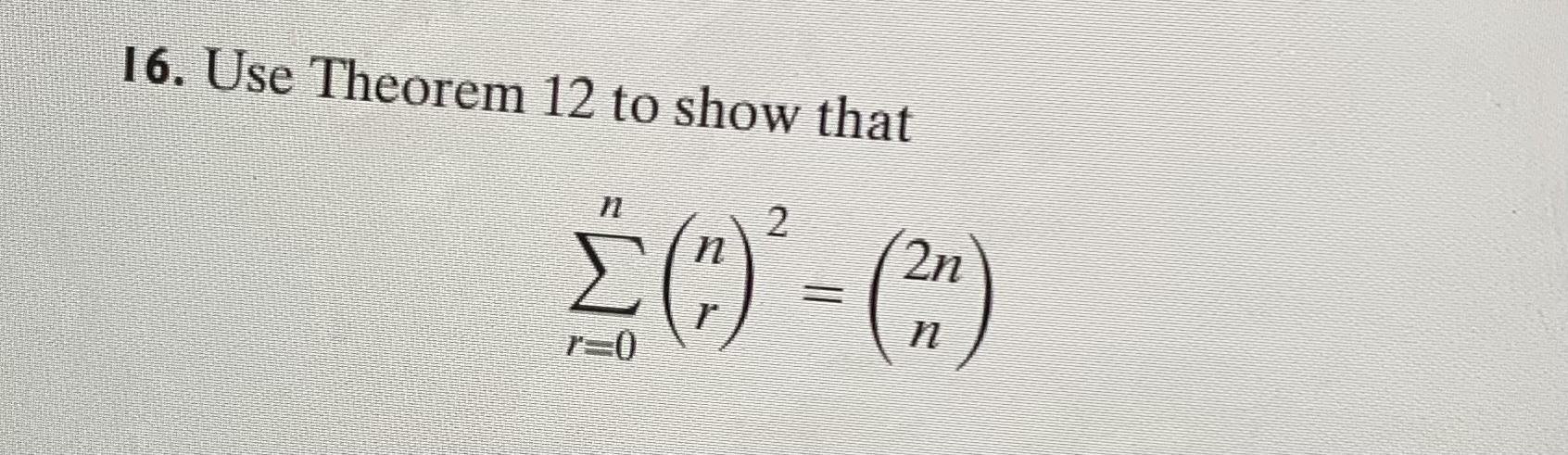
16. Use Theorem 12 to show that 2n In this triangle, the first and last entries of each row are the numeral "1" each other entry in any given row is obtained by adding the two entries in the preceding row immediately to its left and to its right. To state the third theorem about binomial coeffiients, let us make the following definition: () = 0 whenever n is a positive integer and r is a positive integer greater %3D than n. (Clearly, there is no way in which we can select a subset that contains more elements than the whole set itself.) THEOREM 12. k-1 Proof Using the same technique as in the proof of Theorem 11, let us prove this theorem by equating the coefficients of y in the expressions on both sides of the equation (1+y)m+" = (1+y)"(1+y)" m+n' The coefficient of y in (1+y)m+" is ("), and the coefficient of y in k [6)- (1+y)" (1+y)" y+ + %3D ()-) y+ + is the sum of the products that we obtain by multiplying the constant term of the first factor by the coefficient of y in the second factor, the coefficient of y in the first factor by the coefficient of y- in the second factor,..., and the coefficient of y in the first factor by the constant term of the second factor. Thus, the coefficient of y in (1+y)"(1+y)" is () +. and this completes the proof.