probability question

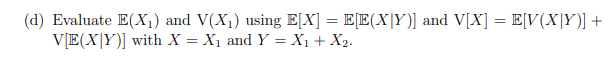
Q1. Let X] = Pn(1) and X2 = Pn(4) be two independent Poisson random variables. Let Y = X] + X2; it is shown on lecture slide 405 that Y = Pn(5). (a) Given Y = n, n 2 0, what are the possible values of X]?(b) Calculate the conditional distribution of X] given Y = n for n 2 0. Specify the distribution and its parameters.(c) Compute the conditional expectation E(X] Y = n), the conditional variance V(Xi|Y = n) for n > 0, and express the conditional mean E(X] Y) and the conditional variance V(X1 Y) as transformations of the random variable Y.(d) Evaluate E(X,) and V(X,) using E[X] = E[E(X|Y )] and V[X] = E[V(X|Y)] + VIE(X|Y)] with X = X1 and Y = X1 + X2